Der goldene Schnitt
Was ist der goldene Schnitt?
Der goldene Schnitt ist ein Verhältnis, das in der Mathematik, Architektur, Kunst und Naturwissenschaften verwendet wird. Es beschreibt das Verhältnis zwischen zwei Größen, bei dem der kleinere Teil zum größeren im selben Verhältnis steht, wie der größere Teil zum Ganzen. Das Teilungsverhältnis wird mit dem griechischen Buchstaben φ (Phi) bezeichnet und hat den gerundeten Wert von 1,618 (bzw. von 1/φ = ~0,618).
Eine Strecke der Länge 1 teilt der goldene Schnitt gerundet bei 0,618. Von den so entstandenen zwei Teilen wird der größere Teil Major genannt und der kleinere Minor. Der Unterschied zwischen dem Goldenen Schnitt und anderen bekannten Teilungsverhältnissen wird im Vergleich klarer. Hier am Beispiel von Halbierung und Drittelung.
Eine Strecke der Länge 1 teilt eine Halbierung bei 0,5. Die so entstandenen zwei Teile werden Hälften genannt.
Eine Strecke der Länge 1 teilt eine Drittelung bei ~0,33 und ~0,66. Die so entstandenen drei Teile werden Drittel genannt.
Warum heißt es "goldener" Schnitt?
Der Name bezieht sich zum einen auf die Tatsache, dass dieses Teilungsverhältnis in der Mathematik als besonders harmonisch und ästhetisch angesehen wird. Zum anderen kommt der goldene Schnitt in der Architektur, der Kunst und der Natur häufig vor und wird daher als besonders "golden" oder "ideal" betrachtet. Alternative Bezeichnungen sind stetige Teilung, Göttliche Teilung, Fibonacci Verhältnis oder Göttliche Proportion (ital. 'Divina proportione').
Wo kommt der goldene Schnitt vor?
Der goldene Schnitt kommt in vielen Bereichen der Natur und der Kunst vor.
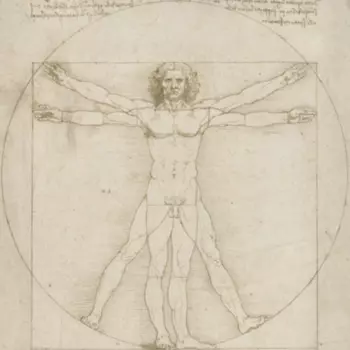
- In der Biologie taucht der goldene Schnitt in der Form von Pflanzen und Tieren auf. Zum Beispiel die Anordnung von Blättern an einem Zweig, oder den Proportionen des Menschen
- In der Mathematik ist der goldene Schnitt unter anderem elementarer Bestandteil der Fibonacci-Zahlenfolge
- In der Malerei und der Fotografie wird er verwendet, um Bildkompositionen auszugleichen und interessanter zu gestalten
- In der Architektur wird er oft verwendet, um Proportionen von Gebäuden und Innenräumen zu gestalten
Daneben gibt es viele weitere Beispiele zum Vorkommen des goldene Schnitts. Er wird oft als ästhetisch ansprechend und harmonisch betrachtet.
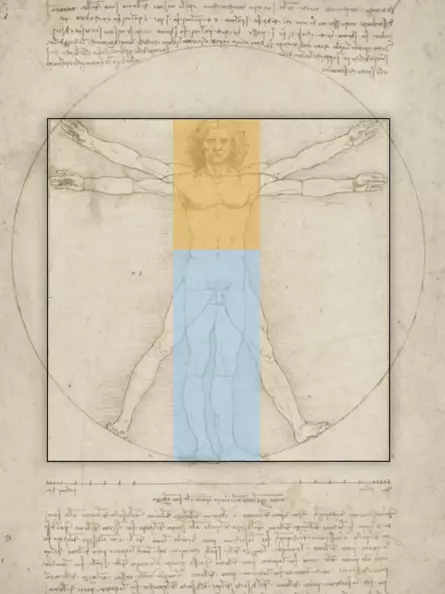
Der goldene Schnitt lässt sich auch in menschlichen Proportionen finden. So befindet sich der Bauchnabel in etwa auf der Höhe des goldenen Schnitts der Körperhöhe
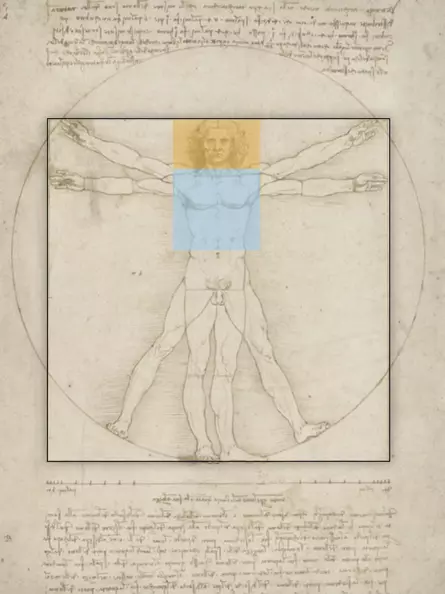
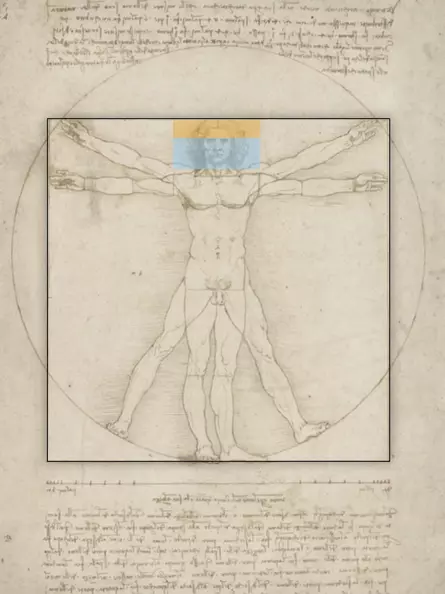

Der goldene Schnitt teilt das Gemälde der Höhe nach und verläuft auf der Höhe der Säulenfüße im Hintergrund. Der Major wird erneut im goldenen Schnitt geteilt und verläuft durch die Augen der Mona Lisa. Ihr linkes Auge befindet sich zudem genau in der Bildmitte (rote Linie)
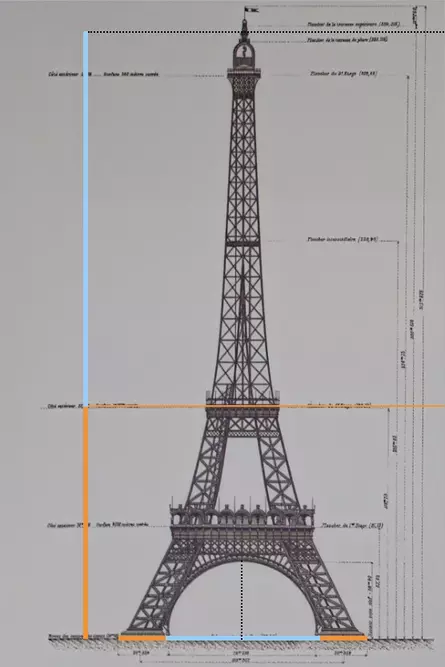
Die mittlere Aussichtsplattform befindet sich im goldenen Schnitt der Turmhöhe (orange Horizontale). Die Breite der Pfeiler am Boden steht im goldenen Schnitt zur Hälfte des Abstands zwischen ihnen (blau/ orange Horizontale)
Die Geometrie birgt zwei große Schätze: der eine ist der Satz von Pythagoras, der andere der Goldene Schnitt. Den ersten können wir mit einem Scheffel Gold vergleichen, den zweiten können wir ein kostbares Juwel nennen.
Goldener Schnitt und Proportion
Eine Proportion ist das Größenverhältnis zweier Teile. Die Besonderheit der Proportion des goldenen Schnitts kann gut im Vergleich zu anderen Größenverhältnissen gezeigt werden. Dafür wird der goldene Schnitt mit der Halbierung und der Dreiteilung verglichen, zwei weiteren häufig verwendeten Proportionen.
Halbierung
Wird eine Strecke von 1 genau in der Mitte geteilt, entstehen zwei gleich große Teile. Jedes der beiden Teile ist genau halb so lang wie die ursprüngliche Strecke. Ihre Länge beträgt jeweils 0,5 (schwarz/graue Streifen).
Goldener Schnitt
Das Besondere am goldenen Schnitt ist, dass das Größenverhältnis des kleineren Teils zum größeren genauso groß ist, wie das des größeren Teils zu der ursprünglichen Strecke. Das heißt, der orange Teil verhält sich zum blauen so, wie der blaue Teil zur Summe aus blau und orange.
Rechnerisch ergibt sich:
blau: ~0,618
orange: 1 - 0,618 = ~0,382
orange zu blau: 0,382 / 0,618 = 0,618
blau zu schwarz: 0,618 / 1 = 0,618
Orange zu blau und blau zu schwarz, haben zueinander also dieselbe Proportion.
Proportion der Unendlichkeit
Die Teilung im goldenen Schnitt kann unendlich fortgesetzt werden. Jeder Teil hat dann zu seinen Teilen dieselbe Proportion. Daher kann auch gesagt werden, der goldene Schnitt ist die Proportion der Unendlichkeit.
Statt der Teilung der Strecke ist auch eine Vergrößerung möglich. Dann muss diese mit 1+0,618 = 1,618 multipliziert werden. Insgesamt entsteht so ein großes Ganzes, dessen Teile als besonders harmonisch erscheinen, weil sie zueinander die gleiche Proportion haben. Das ist nur bei einer Teilung im goldenen Schnitt der Fall.
Dreiteilung
Zur Verdeutlichung eine weitere Proportion, die häufig in der Architektur verwendet wird, die Dreiteilung (rot/ grüne Streifen).
Wird eine Strecke bei einem Drittel geteilt, ergibt sich rechnerisch:
rot: ~0,33 (1/3)
grün: 1 - ~0,33 = ~0,66 (2/3)
rot zu grün: ~0,33 / ~0,66 = 0,5 (1/2)
grün zu schwarz: ~0,66 / 1 = ~0,66 (2/3) ≠ 0,5
Wie bei der Halbierung haben auch hier die Teile zueinander nicht das gleiche Größenverhältnis, wie der größere Teil zum Ganzen.
Varianten des goldenen Schnitts
Goldenes Rechteck
Bei einem goldenen Rechteck stehen die Seitenlängen im Verhältnis des goldenen Schnitts. Es entsteht, wenn der Minor eines goldenen Schnitts um 90° gedreht wird.
Ein goldenes Rechteck kann stets in ein Quadrat und ein kleineres goldenes Rechteck zerlegt werden (Mouseover/Tap).
Goldene Spirale
Eine goldene Spirale entsteht, wenn sich der Radius eines Kreises beim Drehen um den Mittelpunkt alle 90° um den Faktor des goldenen Schnitts verkürzt (Mouseover/Tap). Daher ist sie immer von einem goldenen Rechteck begrenzt.
Eine gängige Annäherungskonstruktion ist die vielfache Zerlegung eines goldenen Rechtecks in immer kleinere goldene Rechtecke. In die dabei entstehenden Quadrate wird jeweils ein Viertelkreis in der Art eingezeichnet, dass er einen bestehenden Viertelkreis fortführt (gelbe Kurve).
Alle goldenen Rechtecke teilen sich nur zwei Diagonalen (gestrichelte Linien). Deren Schnittpunkt ist der Mittelpunkt der Spirale. Die Spirale kann statt von außen zum Mittelpunkt hin auch vom Mittelpunkt nach außen gezeichnet werden, d.h. immer weiter vergrößert werden.
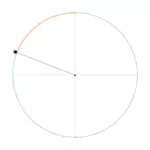
Goldener Winkel
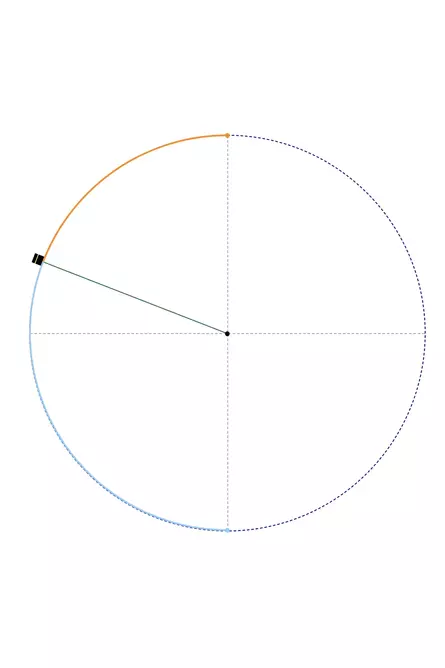
Der goldene Schnitt lässt sich nicht nur aus Strecken bilden. Er kann auch auf den Kreis angewendet werden. Der goldene Winkel entsteht, wenn ein Vollkreis von 360° durch die goldene Zahl geteilt wird. Dabei entstehen zwei Winkel: 360° / ~1,618 = ~ 222,5° und 360° - ~222,5° = ~137,5°. Der kleinere der beiden Winkel wird dabei als goldener Winkel bezeichnet (orange). Nicht nur die Winkel, auch die Längen der so entstandenen Kreisbögen stehen zueinander im goldenen Schnitt (Mouseover/Tap).
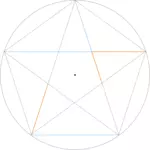
Pentagon, Pentagramm und goldene Dreiecke
Pentagon (altgr. 'Fünf (Eck)winkel') ist die altgriechische Bezeichnung für ein 5-Eck. Meist ist damit jedoch ein regelmäßiges 5-Eck gemeint, das heißt eines, in dem alle Seiten gleich lang sind.
Werden die Eckpunkte mit Diagonalen verbunden, entsteht ein Pentagramm (altgr. 'Fünf Linien'), auch fünfzackiger Stern genannt.
Wichtige Winkel
Vor allem für Bildkompositionen von Gemälden werden häufig die Winkel des regelmäßigen 5-Ecks genutzt:
- 72°, der Mittelpunktwinkel des 5-Ecks
- 108°, der Innenwinkel des 5-Ecks (rechts) und der äußere Winkel zwischen den Zacken des Pentagramms (links)
- 36°, der Innenwinkel der Zacke des Pentagramms
Goldene Dreiecke
In einem regelmäßigen Fünfeck entstehen goldene Dreiecke. Das sind gleichschenklige Dreiecke bei denen die Längen zweier Seiten zueinander im goldenen Schnitt stehen. Es kann nur exakt zwei Formen geben (Mouseover/Tap).
- Innenwinkel Variante 1 (blaues Dreieck): 36°, 72° und 72°
- Innenwinkel Variante 2 (oranges Dreieck): 108°, 36° und 36°
Mythos des 5-Ecks
Ein regelmäßiges 5-Eck kann nur in Kenntnis des goldenen Schnitts konstruiert werden. Dafür dürfen in der klassischen Geometrie nur Zirkel und ein unmarkiertes Lineal verwendet werden.
In der Antike und im Mittelalter war die Konstruktion eines regelmäßigen Fünfecks und damit auch der goldene Schnitt nur einigen wenigen bekannt. Fünfecke galten daher lange Zeit als mystische Geheimzeichen, die nur die verwendeten, die Zugang zu Büchern und Wissen hatten.
Dodekaeder und Ikosaeder (Platonische Körper)
Die platonischen Körper sind nach dem antiken Philosophen Platon benannt (4. Jh. v. Chr.), der sie in seinem Buch Timaios beschrieb. Jeder dieser Körper ist aus denselben regelmäßigen Vielecken zusammengesetzt, wodurch sie eine besonders schöne Symmetrie zeigen. Die platonischen Körper sind Tetraeder (4 gleichseitige Dreiecke), Würfel (6 Quadrate), Oktaeder (8 gleichseitige Dreiecke), Dodekaeder (12 Fünfecke), sowie Ikosaeder (20 gleichseitige Dreiecke). Aus mathematischer Sicht ist besonders, dass es nur exakt diese fünf Körper geben kann, wenn regelmäßige Vielecke lückenlos aneinandergefügt werden sollen.
Das Dodekaeder ist klar mit dem goldenen Schnitt verbunden, denn es besteht aus 12 regelmäßigen 5-Ecken.
Nicht ganz so offensichtlich zeigt sich der goldene Schnitt auch beim Ikosaeder. Denn jeweils fünf seiner 20 Dreiecke berühren sich in einem gemeinsamen Punkt. Dadurch bilden sie regelmäßige 5-Ecke (blau/orange Linien).
Ein weiterer Zusammenhang mit dem goldenen Schnitt zeigt sich in der inneren Struktur eines Ikosaeders, d.h. den Strecken zwischen den voneinander entferntesten gegenüberliegenden Ecken. Denn ein Ikosaeder wird aus drei goldenen Rechtecken gebildet, die so in einen Raum gelegt werden, dass je eines nach der x-, y- und der z-Achse ausgerichtet ist, wobei ihr Schwerpunkt in einem gemeinsamen Punkt liegt, dem Mittelpunkt des Ikosaeders (blaue Rechtecke, Mouseover). Werden die Ecken der goldenen Rechtecke verbunden, entstehen alle Eckpunkte der 20 gleichseitigen Dreiecke eines Ikosaeders (graue Linien).
Beispiele
Ein Ikosaeder kommt in der Natur häufig vor, da es von allen regelmäßigen Polyedern – also den fünf platonischen Körpern – eine Kugel mit gegebenem Durchmesser am platzsparendsten ausfüllt. So haben z.B. Proteinhüllen von Viren (Kapside) in den meisten Fällen die Form eines Ikosaeders.

Beispiele Goldener Schnitt
1
1
2
3
5
8
13
21
34
55
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
1
9
36
84
126
126
84
36
9
1
I Mekka und der goldene Schnitt der Pole
Mekka ist die Geburtsstadt des Propheten Mohammed. Dort befindet sich das zentrale Heiligtum des Islam, die Kaaba. Die geographische Lage von Mekka ist eng mit dem goldenen Schnitt verbunden.
Die geographische Breite von Mekka
Mekka befindet sich etwa auf 21,25° nördlicher Breite (grüne Linie), die Kaaba ca. auf 21,42°. Der Abstand von 1 Breitengrad an der Erdoberfläche ist konstant und beträgt ca. 111,7km.
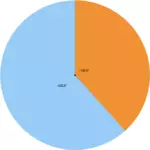
Der Abstand von Mekka zum Südpol (blauer Punkt) beträgt:
(90° + 21,25°) * 111,7km = 12.426,63km (blaue Linie)
Der Abstand von Mekka zum Nordpol (oranger Punkt) beträgt:
(90° - 21,25°) * 111,7km = 7.679,38km (orange Linie)
Beide Strecken stehen zueinander im Verhältnis des goldenen Schnitts:
7.679,38km / 12.426,63 = ~ 0,618
Es ist möglich, dass es sich um eine zufällige Übereinstimmung handelt, da auch viele andere Orte der Erde nahe am goldenen Schnitt zwischen den Polen liegen, z.B. Honolulu auf den Inseln Hawaiis (Breitengrad: 21,3°).

Die Kaaba selbst ist begehbar. Eine große Flügeltür befindet sich ca. 2m über dem Boden und wird nur zu bestimmten Zeiten und nur von bestimmten Personen über eine spezielle Treppe betreten

Der charakteristische Große Rote Fleck des Jupiters befindet sich auf der Südhalbkugel. Es handelt sich um einen gewaltigen Wirbelsturm von etwa 15.000 km Durchmesser, was in etwa dem Erddurchmesser entspricht (ca. 13.000 km). Der Wirbelsturm hält bereits seit Jahrhunderten an und ist der größte im Sonnensystem.
Sein Zentrum liegt nahezu konstant auf dem 22. Breitengrad des Planeten und damit nah am goldenen Schnitt von Nord- und Südpol des Jupiters
Allgemeine Erklärung von Breitengrad und Längengrad
Jeder Ort auf der Welt ist durch Angabe von Breitengrad (Latitude) und Längengrad (Longitude) eindeutig bestimmbar.
Für die Bestimmung des Breitengrades wird eine Linie vom Mittelpunkt der Erde zum Äquator gedacht. Dieser Winkel wurde auf Null festgelegt. Nord- und Südpol liegen nun 90° ober- oder unterhalb des Äquators (nördliche bzw. südliche Breite).
Für die Bestimmung des Längengrades wird in der Draufsicht der Erde eine Linie vom Nord- oder Südpol zum Äquator gedacht. Der Winkel Null wurde 1884 mit dem Nullmeridian festgelegt und verläuft durch Greenwich (England). Jeder Ort auf der Erde befindet sich nun bis zu 180° östlich oder westlich von diesem Ort.
Da der Nullmeridian willkürlich festgelegt wurde und ebensogut durch Tokio oder San Francisco verlaufen könnte, ist der Längengrad im Zusammenhang mit der geographischen Position Mekkas nicht relevant. Anders aber der Breitengrad, der durch Nord- und Südpol der Erde natürliche Bezugsgrößen hat.
Die zwei Nordpole der Erde
Die Erde hat zwei Nordpole. Einen magnetischen Nordpol des Erdmagnetfelds, nach dem sich z.B. eine Kompassnadel ausrichtet. Und einen geographischen Nordpol, der durch die Rotationsachse der Erde bestimmt wird. Die Ausrichtung der Rotationsachse sorgt dafür, dass der Polarstern immer im geographischen Norden liegt. Beide Nordpole wandern, jedoch unterschiedlich schnell, das heißt ihre Position ist nicht fest an einen Ort auf der Erde gebunden.
Der elektromagnetische Nordpol wandert um ein Vielfaches schneller, als der der Rotationsachse. Diese Bewegung varriiert aufgrund physikalischer Prozesse im Inneren der Erde sehr stark. Sie sorgen dafür, dass der elektromagnetische Nordpol aktuell zwischen 0,1° und 0,5° pro Jahr wandert (10km - 50km). Elektromagnetischer Nord- und Südpol der Erde werden daher zukünftig vertauscht sein (Artikel zur Polumkehr, Helmholtz-Gemeinschaft Deutscher Forschungszentren). Da wo heute der elektromagnetische Nordpol liegt, wird in unbekannter Zukunft der elektromagnetische Südpol liegen und umgekehrt. Eine Kompassnadel z.B. zeigt heute nicht mehr auf den geographischen Nordpol der Erdachsenrotation, sondern immer mehr in Richtung des geographischen Äquators, um schließlich auf die Antarktis im geographischen Süden der Erde zu zeigen. Im Lauf der Entwicklungsgeschichte der Erde kam es bereits mehrmals zur Polumkehr. Sie kann sprunghaft und in sehr kurzen Zeitabständen erfolgen. Eine Polumkehr hätte weitreichende Folgen z.B. auf das Klima. Ein Artikel der ESA (European Space Agency) beschreibt das Phänomen.
Der geographische Nordpol der Rotationsachse verändert sich mit etwa 10cm pro Jahr sehr viel langsamer. Das bedeutet, dass er sich in 1000 Jahren um lediglich 100m verschiebt. Er hat seine Ursache in der Präzession der Erde und der ungleichen Verteilung ihrer Massen, z.B. der Ozeane und Kontinente. Der geographische Nordpol ist also eine relativ konstante Größe und dient daher als Grundlage für das Gradnetz der Erde.
II Noahs Arche
Die Maße der Arche Noahs zeigen den goldenen Schnitt.
Noah (auch Noach) ist eine Person des alten Testaments. Seine Geschichte wird zu Beginn von Genesis erzählt, dem ersten Buch der Bibel. Dort rettet er sich und seine Familie, sowie die gesamte Tierwelt in eine Arche, als der biblische Gott alles Leben auf der Erde in einer großen Sintflut vernichtet. Die Arche wird im hebräischen Teyva (תיבה) genannt und bedeutet wörtlich Truhe, Kiste oder Kasten. Ihre Maße werden in der Bibel genannt:
“Mach dir eine Arche aus Zypressenholz! Statte sie mit Kammern aus, und dichte sie innen und außen mit Pech ab!
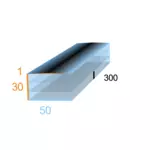
So sollst du die Arche bauen: Dreihundert Ellen lang, fünfzig Ellen breit und dreißig Ellen hoch soll sie sein. Mach der Arche ein Dach und hebe es genau um eine Elle nach oben an! Den Eingang der Arche bring an der Seite an! Richte ein unteres, ein zweites und ein drittes Stockwerk ein!” (gen 6, 14-16).
Die Maße der Arche
Die Arche hatte demnach die Maße des goldenen Schnitts:
- Sie war 300 Ellen lang, 50 Ellen breit und 30 Ellen hoch
- Das Verhältnis der Seitenlängen war damit (durch 10) 30:5:3
- Das Verhältnis von Breite und Höhe war also 3:5 (0,6). Das verweist auf den goldenen Schnitt, denn 3 und 5 sind Fibonacci Zahlen (s. unten)
- Das Dach sollte zusätzlich noch um eine Elle angehoben werden. Die Arche war am höchsten Punkt also 30+1 Ellen hoch
- Das Verhältnis von 31:50 (Höhe des Dachs und Breite der Arche) war demnach 0,62. Das Verhältnis des goldenen Schnitts läge bei ~0,618
- Eine Arche der Breite 1 hatte also mit dem angehobenen Dach eine Höhe zwischen 0,6 (30:50) und 0,62 (31:50)
Der Zahlwert des goldenen Schnitts φ (Phi) liegt bei ~1,618 bzw. 1/φ = ~0,618. Phi ist eine irrationale Zahl mit unendlich vielen Nachkommastellen. Daher konnte der genaue Wert in der Antike nicht berechnet werden. Um dennoch mit irrationalen Zahlen rechnen zu können, wurden sie näherungsweise durch bestimmte Zahlenverhältnisse ausgedrückt. So wurde z.B. die Zahl Pi häufig als 22/7 dargestellt (~3,14). Der Goldene Schnitt hingegen wurde durch zwei aufeinanderfolgende Fibonacci Zahlen ausgedrückt, z.b. 3/5, aber auch 89/144 (s. unten). Um so größer die Fibonacci Zahlen, um so mehr nähern sie sich dem tatsächlichen Zahlwert des goldenen Schnitts an.
III Börsencharts und Fibonacci Retracement
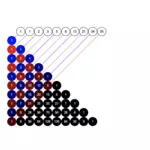
Das Fibonacci Retracement (engl. ‘Fibonacci-Spur Rückverfolgung’) ist eine nach dem mittelalterlichen Mathematiker Fibonacci benannte Methode der technischen Analyse, mit der im Börsenhandel versucht wird, in einem Kurschart zukünftige Kursverläufe vorherzusagen. Dafür werden Unterstützungs- und Widerstandsniveaus mit Hilfe des goldenen Schnitts eingezeichnet. Die Fibonacci-Zahlenfolge ist in diesem Zusammenhang mit dem goldenen Schnitt gleichzusetzen, sie steht im direkten Zusammenhang mit dem goldenen Schnitt (s. unten).
Vorbereitung
- in einem beliebigen Kurschart wird ein Zeitintervall bestimmt
- innerhalb dieses Intervalls wird der höchste und niedrigste Wendepunkt bestimmt (Hoch und Tief, schwarze Kreise)
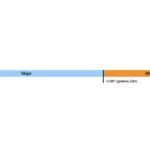
- die Strecke zwischen Hoch und Tief wird im goldenen Schnitt geteilt, einmal nach oben und einmal nach unten (blau/orange, 1. und 2. Streifen von rechts)
- Beide Minor des goldenen Schnitts werden erneut im goldenen Schnitt geteilt, und zwar so, dass da, wo der Minor unten war, er nun oben ist, und da wo er oben war, er nun unten ist (blau/orange, 3. Streifen von rechts)
- der wiederholt durchgeführte goldene Schnitt teilt die Strecke zwischen Hoch und Tief nun bei 23,8 % und 38,2 % und 61,8 % und 76,4%, zusätzlich wird die halbe Höhe bei 50% eingezeichnet
Im professionellen Handel gibt es Tools, die diese Linien automatisiert einzeichnen. Lediglich der Hoch- und Tiefpunkt müssen dafür markiert werden.
Chartanalyse mit dem goldenen Schnitt
Verändert ein Börsenkurs seinen Trend, d.h. einem Allzeithoch folgt eine längere Abwärtsbewegung, vermuten Fibonacci-Händler, dass sich dieser Kursrücklauf an bestimmten Wendepunkten umdrehen wird, nämlich auf einer der Linien des golden Schnitts zwischen Hoch- und Tiefpunkt. Danach muss es ihrer Meinung nach wieder zu einer Aufwärtsbewegung kommen.
Ganz allgemein kann sich der Kurs im Beispielchart (Mouseover) nur in drei Richtungen entwickeln: oben, unten oder seitwärts (rote, grüne und schwarze gestrichelte Linien). Fibonacci-Händler warten nun ab, bis der Kurs erstmals auf eine Linie des goldenen Schnitts trifft (Linie II, orange) und kaufen dann. Steigt der Kurs wieder, gehen sie davon aus, dass die Aufwärtsbewegung anhält und verkaufen frühestens bei der 100% Marke (Linie I, schwarz). Fällt der Kurs aber weiter, verkaufen sie zunächst mit leichten Verlusten und sind dabei der Meinung, der Kurs müsse jetzt bis zur 61,8% Marke fallen (Linie III, orange). Dort wiederholen sie den Kauf und sind der Meinung, der Kurs müsse nun wieder steigen und dann wieder bis zur 100% Marke. Fällt der Kurs jedoch abermals, verkaufen sie erneut mit minimalen Verlusten. Das Fallen auf die 50% Marke (Linie IV, schwarz) ist im Fibonacci Trading ein Anzeichen für bald steigende Kurse und damit grundsätzlich ein Kaufsignal. Fällt der Kurs deutlich unter die 50% Marke, verkaufen sie erneut und setzen nun nicht mehr auf steigende, sondern auf fallende Kurse. Für Aktienbörsen sind z.B. Leerverkäufe eine Möglichkeit, von fallenden Preisen zu profitieren. Sie sind jedoch sehr risikoreich.
Können Börsenkurse vorhergesagt werden?
Grundsätzlich können Kursverläufe nicht vorhergesagt werden. Vielmehr wirken so viele verschiedene Faktoren auf die Entwicklung von Börsenkursen ein, dass mit der heute zur Verfügung stehenden Rechenleistung eine präzise Vorhersage nicht möglich ist. Dennoch wird das Fibonacci Retracement häufig auch von professionellen Großinvestoren angewendet. Denn da so viele Händler sich danach richten, kann der Handel auf Basis des Fibonacci Retracements im Sinne einer selbsterfüllenden Prophezeiung funktionieren. Dass es sich um keine zuverlässige Methode zum Vermögensaufbau handelt, wird an der Tatsache deutlich, dass es aktuell keinen langfristig erfolgreichen Investor gibt, der behaupten würde, diese Handelsmethode wäre die Ursache seines Vermögens.
IV Blüten und der goldene Winkel
Die Spiralen des goldenen Winkels und die Fibonacci Folge
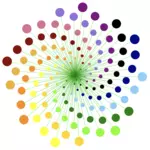
Um einen Mittelpunkt wird ein Winkel von 137,5° gezogen. Der Punkt wird markiert. An diesen ansetzend wird vom Mittelpunkt aus der Winkel erneut gezogen usw. Bei jedem neuen Winkelzug wird der Radius um ein beliebig kurzes Stück verlängert.
Die Zahlen 8, 13 und 21 sind Zahlen der Fibonacci Folge (s. unten). Wird jeder 8., 13. oder 21. Winkel markiert, bilden diese Markierungen ein spiralförmiges Muster. Das spiralförmige Muster tritt nur bei Fibonacci Zahlen auf.




Vorkommen in der Natur
Alle Korbblütlergewächse zeigen den goldenen Winkel. Die Spiralen sind in den Blüten deutlich zu erkennen. Eine solche Verteilung der Blütenblätter sorgt dafür, das auch dicht hinteinander stehende Blütenblätter die maximal mögliche Fläche für die Belichtung erhalten (Mouseover/Tap).
Zu den Korbblütlern gehören z.B. Sonnenblumen, Chrysanthemen, Kamille, Löwenzahn oder auch Kopfsalat.

Der Blütenkorb im Bildzentrum zeigt das spiralförmige Muster des goldenen Winkels

Die Blütenblätter bilden die Spirale des goldenen Winkels
Der goldene Schnitt in der Kunst
Der goldene Schnitt ist nur eine von vielen Proportionen, die in der Kunst verwendet werden. Weil er aber aus mathematischer Sicht die schönste Proportion ist, betont er meistens eine oder mehrere Besonderheiten eines Kunstwerks. Der goldene Schnitt tritt daher selten allein auf und wird typischerweise kombiniert mit weiteren Proportionen wie Drittelungen, Viertelungen usw. Durch eine möglichst vielfältige und spannend arrangierte Komposition soll die bestmöglichst interessante Version eines Kunstwerks erschaffen werden.
Der goldene Schnitt in der Malerei
Der goldene Schnitt wird seit dem Mittelalter in Gemälden verwendet. Er lässt sich in der Bildkomposition, z.B. in der Anordnung der Figuren aufzeigen. Der berühmte Maler Leonardo da Vinci hat sicherlich die beeindruckendsten Kompositionen erschaffen. Er gilt als der beste Maler aller Zeiten und so wundert es nicht, dass auch er den goldenen Schnitt in seinen Gemälden verwendet hat. Oftmals ist zu lesen, der goldene Schnitt wäre hauptsächlich von Renaissance Malern wie Leonardo, Raffael oder Albrecht Dürer verwendet worden. Das ist nicht korrekt, denn der goldene Schnitt lässt über alle neuzeitlichen Epochen hinweg als Teil der Bildkomposition hervorragender Künstler aufzeigen. Damit stellten sie unter Beweis, dass ihre Bildentwürfe nicht nur einer göttlichen Eingebung folgten, sondern dass ihre Kunstwerke zugleich das Werk vernunftbegabter Menschen sind.

Das Format des Gemäldes ist ein goldenes Rechteck. Der goldene Schnitt verbindet die Augen der Madonna und ihre Halsbrosche (Diagonale des Bildformats), das linke Auge des Johannesknaben (goldener Schnitt der Bildhöhe) und das rechte Auge des Jesusknaben (goldene Spirale)

Leonardos letztes Gemälde zeigt 30 Jahre nach der Felsgrottenmadonna den nun erwachsenen Johannes. Sein linkes Auge befindet sich im goldenen Schnitt der Bildbreite, sein Mund im goldenen Schnitt der Bildhöhe

Das linke Ende des Spruchbandes formt eine goldene Spirale

Mit proportionalen Teilungen betont Michelangelo zwei Hände und vier Augen der Dargestellten
Erklärung der fünf oberen horizontalen Linien von oben nach unten:
Linie 1: Die Hand Gottes berührt Adam im goldenen Schnitt der Bildbreite (linke orange Vertikale)
Linie 2: Teilung des Majors von Linie 1 im goldenen Schnitt verläuft unmittelbar neben dem linken Auge des weiblichen Engels (rechte orange Vertikale)
Linie 3: Halbierung des Minors von Linie 2 verläuft durch das linke Auge des Engels am rechten Bildrand (rechte weiße Vertikale)
Linie 4: Halbierung des Majors von Linie 2 verläuft durch das linke Auge Gottes (linke weiße Vertikale)
Linie 5: Drittelung des Minors von Linie 1 führt zum rechten Auge Adams (grüne Vertikale)
Links vom primären Goldenen Schnitt bei der Hand Gottes wird das rechte Auge Adams betont, auf der rechten Seite die linken Augen der Figuren.
Auch in Bezug auf die Bildhöhe lässt sich die Verwendung der klassischen geometrischen Proportionen aufzeigen (Mouseover). Erklärung der vier vertikalen Linien von links nach rechts:
Linie 1: Das Auge Gottes befindet sich auf 1/4 der Bildhöhe (untere weiße Horizontale)
Linie 2: Das linke Auge des Engels am rechten Bildrand befindet sich auf 1/3 der Bildhöhe (grüne Horizontale)
Linie 3: Das rechte Auge Adams befindet sich im goldenen Schnitt der Bildhöhe (orange Horizontale)
Linie 4: Das Auge des weiblichen Engels befindet sich auf 5/12 des Minors von Linie 3 (obere weiße Horizontale). Der Blick des weiblichen Engels verfehlt den Gehörgang Gottes knapp, tatsächlich schaut sie vielmehr auf Gottes Kopf im Ganzen

Masaccios Fresko gilt als eines der ersten Gemälde mit korrekt dargestellter Zentralperspektive. Es wird von einem goldenen Rechteck umspannt. Wird die Höhe dieses Rechtecks im goldenen Schnitt geteilt führt dies zu den Kapitellen der Säulen des vorderen Bogens (obere orange Horizontale). Der goldene Schnitt der Höhe dieser Säule führt zu den Kapitellen des hinteren Bogens (untere orange Horizontale). Der Querbalken des zentralen Kreuzes befindet sich im goldenen Schnitt der Höhe des vorderen Bogens (Mouseover/Tap)

Manet gilt als einer der Wegbereiter der modernen Malerei.
In dem Gemälde verläuft der goldene Schnitt der Bildbreite durch das rechte Auge des Herren und betont außerdem seinen Ringfinger (orange Vertikale). Der goldene Schnitt ist nicht die einzige Proportion in dem Gemälde, z.B. verläuft die Hälfte der Bildhöhe exakt entlang der Banklehne, auch befindet sich das linke Auge des Herren genau auf 2/3 der Bildbreite (Mouseover/Tap).
In Bezug auf die Bildhöhe verläuft der goldene Schnitt am oberen Rand zweier Vasen im Hintergrund (untere orange Horizontale, blaue und beige Vase). Wird der Major erneut im goldenen Schnitt geteilt, verläuft er knapp über dem rechten Auge der Dame, trifft ihr linkes Auge jedoch genau (obere orange Horizontale).
Der so entstandene Zusammenhang von Vase am linken Bildrand und ihrem linken Auge erinnert stark an den goldenen Schnitt in der Mona Lisa (linker Säulenfuß und linkes Auge). Das führt zu der Vermutung die zwei Gemälde könnten auch hinsichtlich der Bildidee in Verbindung stehen, was allerdings weiter untersucht werden sollte. Wie jeder berühmte Maler hat sich auch Manet mit Leonardo auseinandergesetzt, weil er unter anderem aufgrund seiner geometrischen Kenntnisse im Hinblick auf die Bildkompositionen bis heute als der einfallsreichste Maler gilt. Dass Manet Elemente aus Leonardo-Gemälden zitiert, wird bei einem weiteren Gemälde deutlich, der 'Blonde Woman with Bare Breasts', das eine bissige Parodie auf Leonardos Dame mit dem Hermelin darstellt

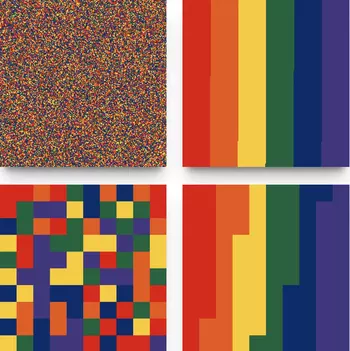
Rothko war ein abstrakter Maler und Wegbereiter der Farbfeldmalerei.
Gedanklich teilte er das Gemälde vertikal in 24 Einheiten (schwarz/weißer Streifen). Nach oben und unten haben die Farbfelder einen Abstand von 1/24 bzw. 2/24 (Mouseover Tap). Auf das untere schwarze Farbfeld aufsetzend (weiße Horizontale), werden die zwei darüberliegenden Farbfelder in einer Höhe von 13/24 im goldenen Schnitt bei 5/24 geteilt (orange Horizontale). Somit ist das obere schwarze Farbfeld 8/24 hoch (blau). 5, 8 und 13 sind Fibonacci Zahlen. Fibonacci Zahlen stehen in einem direkten Zusammenhang mit dem goldenen Schnitt (s. unten)
Der goldene Schnitt in der Fotografie
Der goldene Schnitt wird als eine von vielen Proportionen in der Komposition von künstlerisch wertvollen Fotografien analog zur Malerei verwendet. Dazu sollten die Elemente des Bildmotivs, die sich im goldenen Schnitt befinden sollen, statisch sein, bei bewegten Objekten ist es eine Frage des Timings. Sollen sich Elemente in bewegten, also dynamischen Motiven im goldenen Schnitt befinden, müssen sie meist im Nachgang entsprechend beschnitten werden. Es versteht sich von selbst, dass geometrisch-komplexe Bildkonstruktionen dann entweder zufällig oder schlicht nicht möglich sind.
In der Amateurfotografie bzw. bei dynamischen Motiven (Schnappschüsse) ist es schwer den goldenen Schnitt bei Aufnahmen zu berücksichtigen. Dafür müsste im Bildsucher ein Raster eingeblendet sein, dass das Motiv mit Hilfslinien überlagert. Das Teilungsverhältnis des goldenen Schnitts (~0,618) liegt recht nah an einem weiteren häufig verwendeten Teilungsverhältnis, dem Verhältnis von 2:3 (~0,666). In der Praxis wird daher statt dem schwer abzuschätzenden goldenen Schnitt meist die Drittelregel angewendet. Daher zeigen die Displays von Digitalkameras (beziehungsweise Handys im Fotomodus) meist drei Felder neben- bzw. übereinander an, die die Drittellinien kennzeichnen. Um spannende Bildausschnitte zu erreichen, kann es hilfreich sein, die zu fotografierenden Objekte entlang dieser Drittellinien zu positionieren, statt direkt in der Bildmitte.
Ebensogut könnten statt den Drittellinien auch die Hilfslinien des goldenen Schnitts eingeblendet werden, was einige Hersteller optional unterstützen. Wie für die Malerei gilt auch hier, dass eine Fotografie in ihrer Bildkonstruktion nicht nur eine Proportion zeigen sollte. Vielmehr zeigen professionelle Fotografien ein Zusammenspiel verschiedener Proportionen, um die jeweilige Bildaussage zu unterstützen.

Karl Marx begründete die philosophische Schule des Kommunismus. Er war auch als politischer Journalist aktiv und beschäftigte sich mit den historischen Zusammenhängen von Revolutionen.
Das Format der Fotografie ist ein goldenes Rechteck. Das Bildmotiv (Raum, Vorhang, Person, Stuhl und Hut) wurde sorgfältig arrangiert
- der zurückgezogene Vorhang befindet sich auf 1/3 der Bildbreite, ebenso wie der Dargestellte (linke grüne Vertikale)
- das linke im Schatten liegende Auge von Karl Marx befindet sich knapp neben der Bildmitte (linke rote Vertikale) und ebenso knapp unter dem goldenen Schnitt der halben Bildhöhe (obere orange Horizontale)
- seine Rechte Hand liegt auf halber Bildhöhe auf der Stuhllehne und endet am rechten Drittel des Bildes (rechte grüne Vertikale), der goldene Schnitt der Bildbreite betont seinen Ringfinger (orange Vertikale)
- die Stuhllehne hinter der Marx steht, wird nach links vom goldenen Schnitt der Bildbreite begrenzt (orange Vertikale), das obere Ende des Stuhls befindet sich auf halber Bildhöhe (obere rote Horizontale) und nach rechts wird die Stuhllehne vom rechten Viertel des Bildes begrenzt (rechte rote Vertikale)
- die Stuhllehne trennt ihn im goldenen Schnitt von einem Hut, der auf dem unteren Viertel der Bildhöhe liegt, eine Kopfbedeckung, scheinbar achtlos auf die Sitzfläche geworfen (mittlere rote Horizontale)
- wird die Höhe unter dem Hut im goldenen Schnitt geteilt, endet dort die leere Wand (untere orange Horizontale). Marx steht mit den Hacken an der Wand
- auf halber Höhe des Majors geht der Fußboden zur Fußbodenleiste über (untere rote Horizontale)

Sigmund Freud gilt als Begründer der Psychoanalyse. Er forschte auch zur menschlichen Sinneswahrnehmung und entwickelte eine eigene Triebtheorie. Seine Methoden waren nicht unumstritten, so setzte er neben dem aktiven Zuhören unter anderem auf die sexuelle Befreiung der Frauen, Kokain und Hypnose als therapeutische Methoden.
Das Format des Bildes ist 3:4. Auch wenn die Szene durch die brennende Zigarre beiläufig erscheint, nahm Freud die Pose nicht zufällig ein.
- im linken Drittel des Bildes (linke grüne Vertikale) hält Freuds rechte Hand eine abbrennende Zigarre. Sie befindet sich auf halber Bildhöhe (rote Horizontale) und im ersten Viertel des Bildes (linke rote Vertikale)
- Freuds linkes Auge befindet sich knapp neben der Bildmitte (rechte rote Vertikale) und ebenso knapp unter dem goldenen Schnitt der halben Bildhöhe (obere orange Horizontale)
- Freuds linker Gehörgang liegt im goldenen Schnitt der Bildbreite, zudem wird das Ohr nach rechts vom rechten Drittel der Bildes begrenzt (rechte grüne Vertikale)
- Freuds Mund befindet sich genau auf dem goldenen Schnitt der halben Bildhöhe (mittlere orange Horizontale)
Freuds rechtes Auge liegt im Schatten. Überhaupt betont das starke künstliche Licht seinen Schatten an der Wand (Mouseover).
Insgesamt betont die proportionale Einteilung des Bildes die fünf menschlichen Sinne: das Sehen des Auges, das Hören des Ohres, das Riechen der Nase (Qualm der Zigarre) und das Schmecken des Mundes. Der Tastsinn als fünfter und letzter Sinn wurde über keine der gängigen Proportionierungen betont. Es liegt nahe, ihn bei seiner linken Hand zu vermuten, die sich im rechten Drittel des Bildes auf seine Hüfte stützt
- Freuds graubärtiges Kinn wird vom goldenen Schnitt der Bildhöhe exakt tangiert (untere orange Horizontale)

Edward Steichens Fotografien hatten maßgeblichen Einfluss auf nachfolgende Fotografen. Sein Gesamtwerk ist äußerst vielschichtig. Vor allem in der Porträtfotografie hat er die Motive nach elegant konstruierten geometrischen Regeln konstruiert, um die jeweilige Bildintention zu unterstreichen.
Das Format des Bildes ist 4:5
- die Naseneingänge der sehr kultiviert wirkenden Dame, (Mouseover/Tap) befinden sich im goldenen Schnitt der Bildbreite (rechte orange Vertikale)
- der goldene Schnitt der Bildhöhe führt genau über ihre linke Schulter, wo das schwarze Kleid den Blick auf ihren Hals freigibt (unterste orange Horizontale)
- ihre Hände führen zu einer Blume, die sich zwischen ihren Händen mittig am unteren Bildrand befindet (rote Vertikale). Die Mittelhalbierende schneidet zudem die Spitze ihres linken Zeigefingers (blauer Punkt).
Der Zeigefinger ist eine Anspielung auf die traditionelle christliche Ikonographie, vor allem die Johannes des Täufers, der häufig mit zum Himmel deutenden Zeigefinger dargestellt wird. Die berühmteste Darstellung stammt von Leonardo da Vinci, dessen Gemälde "Johannes der Täufer" ebenso wie diese Fotografie im Format von 4:5 angelegt wurde. Überhaupt erinnert Steichens Bildmotiv sehr an Leonardos berühmte Zeichnung "Il Condottiere" (dt. 'Der Söldnerhauptmann'), die durch einen sehr markanten Helm und eine fantasievolle Brustrüstung bekannt ist
- der modische Hut (ohne die aufgesetzten Blumen) befindet sich genau im mittleren Drittel der Bildbreite (grünschattierte Vertikalen)
- ein goldener Schnitt im linken Drittel der Bildbreite markiert eine Struktur im Hintergrund, die nur verschwommen zu erkennen ist (möglicherweise ein Türrahmen oder eine Zierleiste, linke orange Vertikale)
- diese Struktur wiederum wird durch einen dunkleren einfarbigen Streifen am linken Bildrand ebenfalls im goldenen Schnitt geteilt (orange/ blaue Fläche, Mouseover)
- im Hintergrund des rechten Bildrands befindet sich ein schattierter Bereich (pink/ blaue Fläche, Mouseover), möglicherweise Raumecken. Er wird im Wurzel aus 2 Verhältnis geteilt (1 geteilt durch Wurzel aus 2 = ~0,71) und nimmt damit Bezug auf ein Quadrat. Das Wurzel 2 Verhältnis ist auch als DIN A4 Verhältnis bekannt (DIN A4 Breite geteilt durch DIN A4 Höhe). Es wird in der Kunst jedoch nur sehr selten eingesetzt. Warum Steichen es hier so beiläufig einsetzte, bleibt im Dunklen
- oberhalb des goldenen Schnitts der Bildhöhe (unterste orange Horizontale) kommt es zu drei ineinander verschachtelten Teilungen im goldenen Schnitt (sogenannte stetige Teilung), die vor allem den modischen Hut in Szene setzen
1. die erste Teilung verläuft knapp unterhalb der im Schatten liegenden Augen (2. untere Horizontale, orange)
2. die zweite Teilung betont die obere Hutkante (oberste orange Horizontale)
3. die dritte Teilung betont die vordere Kante des Hutes (3. untere Horizontale, orange)
Insgesamt beweist die verspielte Fotografie für ein Modemagazin eine künstlerische Absicht des Fotografen. Dass Edward Steichen sich dabei von Leonardos Zeichnung "Il Condottiere" inspirieren ließ, darf vermutet werden.
Die finale Unterteilung des Hutes demonstriert zum einen die sehr detailbewusste Vorgehensweise Steichens bei der Bildkomposition. Zum anderen wird auch hier klar, dass das Foto nicht durch einen spontanen Schnappschuss entstanden sein kann, sondern dass das Kunstwerk das Ergebnis einer vorangegangenen Planung gewesen sein muss. Für die praktische Umsetzung nutzte Steichen entweder Markierungen im Bildsucher des Fotoapparats, oder Markierungen an Maßstäben außerhalb des Bildraums.


Diese Schlüsselszene zählt zu den berühmtesten Szenen der Filmgeschichte. Sie spielt vor dem Hintergrund des Sonnenaufgangs an der Atlantikküste bei New York (Mouseover). Der Börsentycoon Gordon Gekko (Michael Douglas, hier im Bild) ruft den Börsenhändler Bud Fox (Charlie Sheen) an und teilt ihm mit, dass er eine größere Summe seines Vermögens verwalten darf. Gekkos einleitendes "Money never sleeps, pal" (engl. 'Geld schläft nie, Kumpel') drückt den Zeitgeist einer ganzen Generation zur Zeit des US-amerikanischen Wirtschaftsaufschwungs in der Reagan Ära aus (1980-88). "Wall Street: Money never sleeps" ist zugleich der Titel der 23 Jahre später entstandenen Fortsetzung von 2010, erneut von Oliver Stone und wieder mit Michael Douglas (außerdem Shia LaBeouf).
Das betont die große Bedeutung speziell dieser Szene im Werk von Oliver Stone, der "Wall Street" seinem verstorbenen Vater widmete. Louis Stone war viele Jahre als Börsenhändler tätig gewesen, musste aber wegen einiger Fehlspekulationen Bankrott anmelden.
Im Schlussdialog der Szene wechselt Gordon Gekko plötzlich das Thema und beginnt von der Schönheit des Sonnenaufgangs zu sprechen: "Ist das toll. Wenn du das sehen könntest. Jetzt geht die Sonne hier auf. Ich habe noch nie ein Bild gesehen, dass diese Schönheit einfangen konnte".
Gekko dreht sich währenddessen zum Meer hin, so dass sich die Sonne hier im Bild rechts hinter ihm befindet. Im Kontext des Films müsste er sich auf seinem Anwesen an der Ostküste der USA befinden, dann würde sich die Sonne beim Sonnenaufgang aber direkt vor ihm befinden, stattdessen ist sie hinter ihm. Er blickt also in westlicher Richtung auf ein Meer, z.B. den Pazifik an der Westküste der Vereinigten Staaten bei Hollywood, Los Angeles. Die versteckte Symbolik ist vermutlich kein Filmfehler, denn die westliche Himmelsrichtung ist in der Kunst von alters her mit dem Tod verbunden, da dort die Sonne untergeht. Unter anderem ließen sich die ägyptischen Pharaonen deswegen ausschließlich auf der westlichen Nilseite bestatten. Der Blick auf den Strand, ein einsamer Mann und das ewige Meer müssen daher im Kontext von Oliver Stone und seinem Vater betrachtet werden: auf der einen Seite der Vater, einst ein New Yorker Börsenhändler an der Ostküste und auf der anderen Seite sein Sohn, ein erfolgreicher Regisseur in Hollywood an der Westküste der USA.
Das letzte Bild der Szene ist streng nach dem goldenen Schnitt gegliedert. Dafür wurde die Kamera in eine bestimmte Höhe gebracht, um die Horizontlinie festzulegen (Kamerawinkel). Die Entfernung der Kamera bestimmt Breite und Höhe der Figur links im Bild. Der Höhe nach teilt der Horizont das Bild im goldenen Schnitt (orange Horizontale, Mouseover). Gordon Gekkos Position wurde nach dem goldenen Schnitt bestimmt (die Hälfte der dritten Teilung im goldenen Schnitt der Bildbreite, rote Vertikale). Bemerkenswerterweise macht Gekko, nachdem er einige Sekunden so verharrt, ohne erkennbare Ursache und fast wie auf Regieanweisung in der letzten Sekunde der Einstellung einen leichten Ausfallschritt nach links (Mouseover). Dadurch wird sein Körper nicht mehr von der roten Linie geschnitten und er befindet sich nun direkt links von ihr. Die brandenden Wellen des Meeres bilden das dynamische Element in dieser filmischen Fotografie.
Die 55. Filmminute der Szene steht zur Gesamtlänge des Films (120 Minuten) nicht im goldenen Schnitt (55/120= ~0,45), allerdings ist die 55 eine Fibonacci Zahl. Fibonacci Zahlen stehen direkt mit dem goldenen Schnitt in Verbindung (s. unten). Das Fibonacci Retracement wird etwa seit den 1930er Jahren für Analysen von Börsenscharts verwendet (s. oben). Ebenso wie in diesem Szenenbild werden dort standardmäßig drei Teilungen des goldenen Schnitts und eine Halbierung verwendet, um Börsencharts zu analysieren (bei 23,6%, 38,2%, 50% und 61,8%), dort jedoch in der Höhe und hier in der Breite. Die Positionierung der Person am Strand nimmt damit klar Bezug auf den Beruf des verstorbenen Vaters von Oliver Stone.
"Ich hab dir gezeigt, wie das Spiel läuft. Jetzt ist die Schule zu Ende" (Gordon Gekko, ebenfalls in der Szene)
Der goldene Schnitt in der Architektur
Der goldene Schnitt wird seit der Antike in der Architektur verwendet. Bestimmte Pyramiden in Ägypten sollen diese Proportion aufweisen. Da die Pyramiden durch Erosion und Materialraub über die Jahrtausende ihr Aussehen jedoch stark verändert haben, ist dies nicht mehr zweifelsfrei nachzuweisen. Als älteste gesicherte Belege zur Verwendung des goldenen Schnitts in der Architektur gelten die Bauten der griechischen, sowie der römischen Antike. Der goldene Schnitt ist spätestens seitdem eine der vielen Proportionen die Architekten bei der Konstruktion von Bauwerken nutzen. Er lässt sich in der Fassadengestaltung mittelalterlicher Kirchen aufzeigen, in Renaissance Bauten und ist bis in die heutige Zeit hinein eine der meistverwendeten Proportionen, beim Entwurf bzw. der Proportionierung von Gebäuden.
Wichtig ist die Feststellung, dass der goldene Schnitt nie die einzig verwendete Proportion beim Entwurf eines Bauwerks ist. Vielmehr sind Bauwerke, ebenso wie Gemälde das Resultat vom Zusammenspiel verschiedener Proportionen, wie z.B. Halbierung, Drittelung oder Viertelung. Die Besonderheit des goldenen Schnitts liegt in seiner mathematischen Eigenschaft, immer wieder in sich selbst geteilt werden zu können, wobei seine Teile immer das gleiche Verhältnis zueinander behalten, nämlich das des goldenen Schnitts. Diese Schönheit stellt etwas besonderes und einzigartiges dar, weswegen der goldene Schnitt als Gestaltungselement meist sehr akzentuiert eingesetzt wird, um bestimmte Gebäudeteile, markante Elemente bzw. deren Funktion zu betonen. Beispiele für die Verwendung des goldenen Schnitts sind die Chephren-Pyramide, das Athener Parthenon, der Pariser Eiffelturm und das Hauptquartier der Vereinten Nationen in New York.
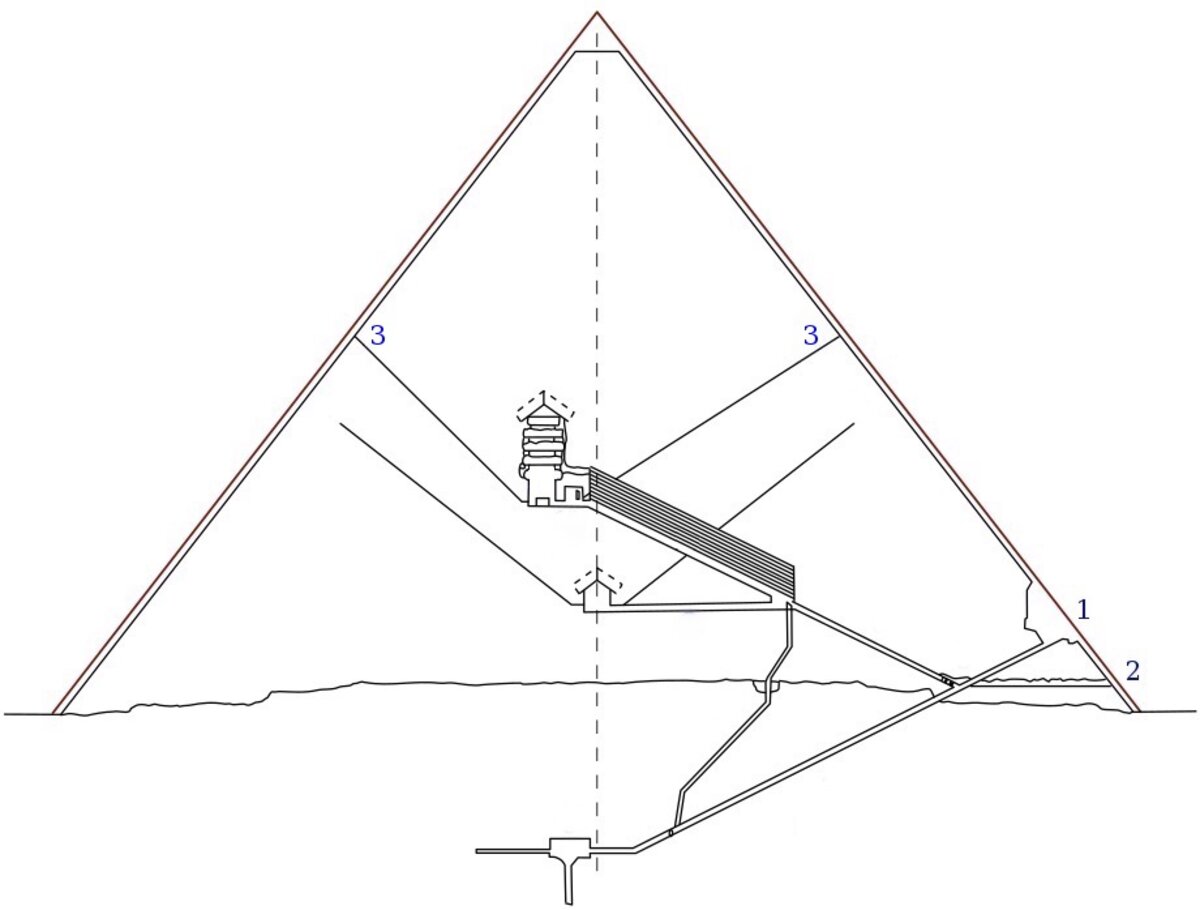
Die ursprünglichen Maße der Chephren Pyramide lassen sich heute nicht mehr genau bestimmen. Grundsätzlich gibt es zur Annahme der Verwendung des goldenen Schnitts in dem Bauwerk zwei Varianten, die sich jedoch gegenseitig ausschließen.
Entweder steht die Seitenlänge zur halben Länge der Basis im goldenen Schnitt, dann läge der Neigungswinkel der Pyramide etwa bei 51,8°.
Oder aber der Neigungswinkel der Pyramide betrug ursprünglich 54°, wodurch die Spitze der Pyramide den Mittelpunktwinkel eines regelmäßigen 5-Ecks bilden würde (72°, Mouseover/Tap). Dann stünden aber Seitenlänge und halbe Basislänge nicht zueinander im goldenen Schnitt. Dass die beiden in Frage kommenden Neigungswinkel so nah beieinander liegen, ist die Ursache für den Streit der Ägyptologen über die Absicht der damaligen Baumeister.
Da die Pyramiden ursprünglich eine weiße Kalksteinverkleidung hatten und sich auf der Spitze ein weithin sichtbarer goldener Schlussstein befand, ist es wahrscheinlicher, dass der Neigungswinkel 54° betrug, um mit dem finalen 5-Eck die Spitze des weithin strahlenden Bauwerks zu betonen (Mouseover). Dann würde die Pyramide die drei grundlegenden geometrischen Figuren der klassischen Geometrie vereinen: ein quadratischer Grundriss, eine nach oben strebende Dreiecksform, die von einem Fünfeck gekrönt wird.
Zudem haben mehrere der zehn größten Pyramiden heute einen Neigungswinkel (Böschungswinkel) von etwa 51°-53°, was dafür spricht, dass der von den Baumeistern ursprünglich angestrebte Böschungswinkel 54° betrug. Dass der Böschungswinkel einer Pyramide für die Ägypter wichtig war, zeigt die etwa 75 Jahre ältere Knickpyramide von Pharao Snofru (Vater von Pharao Cheops). Sie war die erste echte Pyramide, das heißt ohne Stufen und mit geraden Seitenkanten. Sie wurde bis zur halben Höhe etwa im Winkel von 60° gebaut, dem Innenwinkel eines gleichseitigen Dreiecks. Aufgrund der Einsturzgefahr wurde in einer zweiten Phase versucht ein flacherer 54° Winkel zu erreichen, dem halben Innenwinkel eines regelmäßigen 5-Ecks (Mouseover), um schließlich in einer dritten Phase eine Pyramide im ca. 45° Winkel aufzusetzen (43°), dem halben Innenwinkel eines regelmäßigen 4-Ecks (Quadrat). Die Snofru Pyramide vereint somit ein regelmäßiges 3-,4- und 5-Eck in einem Bauwerk und macht es sehr wahrscheinlich, dass die geometrischen Kenntnisse der ägyptischen Baumeister die Konstruktion des goldenen Schnitts einschlossen.
Möglicherweise handelt es sich aber auch um zufällige Übereinstimmungen, da spätere Baumeister, z.B. beim Tempelbau andere Proportionen nutzten.

Das Parthenon wurde um 450 v.Chr. anlässlich des Endes der Perserkriege errichtet und der Schutzgöttin von Athen gewidmet, Athene. Kurz nach dem Bau des Tempels wurde der bedeutende Philosoph Platon in Athen geboren (um 427 v. Chr.). In seinen mathematischen Schriften äußert er sich u.a. zum goldenen Schnitt.
Die Fotografie gibt die Proportionen der Ostfassade des Parthenons leicht verfälscht wieder. Grundsätzlich ist die Ostfassade als goldenes Rechteck angelegt, wobei die Höhe des Fundaments mitgerechnet wird. Die rekonstruierbare Silhouette des teils zerstörten Dachs wird hier mit schwarzen Linien angedeutet. Das Dach setzt auf den Kapitellen der Säulen auf, die sich im goldenen Schnitt der Gebäudehöhe befinden.
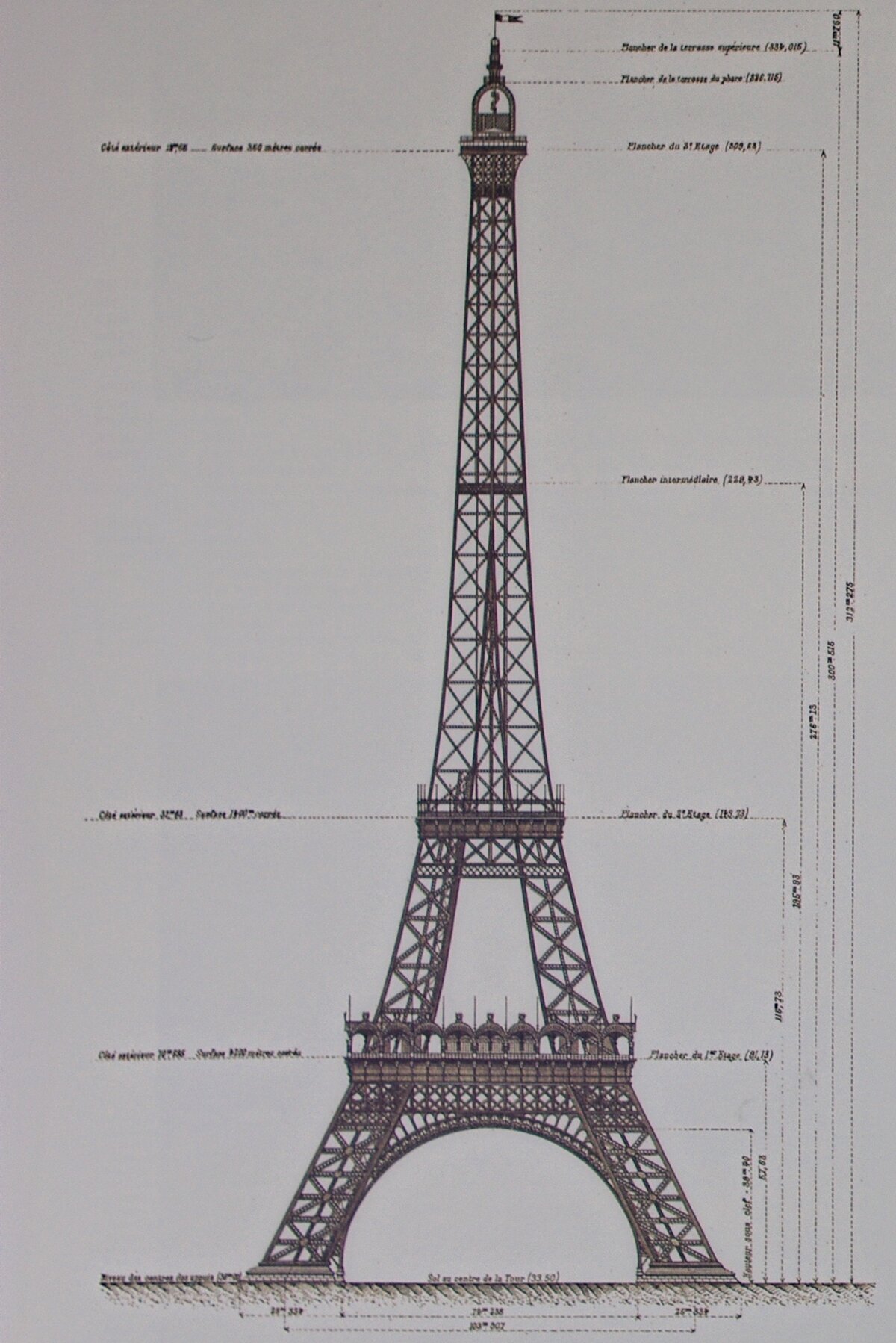
Gustav Eiffel, der ausführende Architekt des 1889 errichteten Turms, zeigt diese maßstabsgerechte Skizze in seinem 1900 erschienenen Buch "La tour de trois cents mètres" (frz. 'Der Turm der 300 Meter').
- das Fundament hat zur ersten Plattform denselben Abstand, wie die erste Plattform zur zweiten (rechter schwarz/weißer Streifen)
- die vier Säulen des Turms laufen in einer markanten Ringfassung zusammen. Sie markiert die Hälfte der Strecke von der zweiten Plattform bis zur dritten Plattform bei der Turmspitze (linker schwarz/weißer Streifen)
- insgesamt wird die Höhe des Turms bei der zweiten Plattform im goldenen Schnitt geteilt (blau/orange Vertikale)
Gustav Eiffel zeichnete in der Turmspitze ebenfalls Proportionen ein, unter anderem legte er die Maße der Fahnenstange fest. Da die Spitze des Turms häufiger modernisiert wurde, ist seine ursprüngliche Idee jedoch im Laufe der Zeit verlorengegangen.
Interessant ist, wie Eiffel mit dem Kreisbogen im unteren Teil des Turms spielt. Seine Höhe entspricht fast einem goldenen Schnitt in Bezug auf den Abstand von Fundament und erster Plattform (grün/roter Streifen). Tatsächlich beträgt sie aber 2/3, also ~0,666 statt 0,618
- dennoch findet sich in diesem Bereich ein goldener Schnitt: Die Summe der Breite der Standfüße des Turms ist ein goldener Schnitt zum Durchmesser des Kreisbogens (blau/orange Horizontale). Wird die Strecke mittig geteilt, liegen zwei Strecken nebeneinander, die im goldenen Schnitt geteilt wurden (Mouseover/Tap)
- die erste Plattform ist die breiteste, die zweite Plattform genau halb so groß (schwarz/weiße Horizontalen). Anhand der Skizze ist nicht zu sagen, ob die dritte Plattform an der Spitze erneut halb so groß sein sollte, wie die zweite. Das Verhältnis beträgt in dieser Darstellung nur ~46% (statt 50%). Dasselbe gilt für das Verhältnis der Breite des Fundaments und erster Plattform, das dem goldenen Schnitt mit ~0,595 nur sehr nahe kommt (statt 0,618)
Abschließend kann festgestellt werden, dass der Eiffelturm wegen seinen schlichten Eleganz ein gelungenes Beispiel für überlegte Proportionierung ist. Es ist außerdem deutlich geworden, dass nicht allein der goldene Schnitt die Ästhetik der Komposition eines Kunstwerks verursacht. Sondern diese Form der Ästhetik entsteht im Zusammenspiel verschiedener Proportionen.

Die Frontfassade bildet ein goldenes Rechteck.
Um 1947 wurde das Gebäude unter Führung der beiden Stararchitekten Le Corbusier und Oscar Niemeyer entworfen.
Vor allem der Franzose Le Corbusier (1887-1965) wandte zeitlebens den goldenen Schnitt an, und entwickelte ein eigenes darauf basierendes Maßsystem, das er in vielen seiner berühmten Gebäude verwendete, den Modulor.
Der Brasilianer Oscar Niemeyer (*1907), war unter anderem der verantwortliche Architekt der öffentlichen Gebäude bei der Gründung von Brasilia, der Hauptstadt Brasiliens. Er starb 2012 im Alter von 104 Jahren.
Der goldene Schnitt in der Typographie
Mit der Erfindung des Buchdrucks entstand die Notwendigkeit einheitliche Gestaltungsprinzipien für die Lettern zu entwickeln. Lettern sind einzelne Metall- oder Holzbuchstaben, die auf einer Druckplatte zu Texten angeordnet werden und dann gedruckt werden. Gestaltungsprinzipien für die Lettern sollten zum einen die Lesbarkeit und Ästhetik der gedruckten Buchstaben sicherstellen und zugleich Varianz ermöglichen. Zum anderen sollte durch diese Regeln sichergestellt werden, dass die einzelnen, sich schnell abnutzenden Letter der Druckplatten möglichst einfach reproduziert werden konnten. Aufwändige und besonders kunstvoll gestaltete Lettern mit individuellen filigranen Verzierungen, die nur von speziell ausgebildeten Handwerkern hergestellt werden konnten, waren daher nicht praxistauglich.
Einen ersten bedeutenden Schritt in Richtung einheitlicher Regeln für das Erscheinungsbild von Buchstaben unternahm Luca Pacioli (1445-1517). Als Schüler des herausragenden Renaissancemalers Piero della Francesca, der neben seinen malerischen Werken auch für seine mathematischen Abhandlungen bekannt war, wurde Pacioli einer der herausragenden Mathematiker seiner Zeit, so ist er unter anderem für die erstmalige Veröffentlichung der bahnbrechenden Methode der doppelten Buchführung bekannt. Am Mailänder Hof arbeitete er eng mit Leonardo da Vinci zusammen.
Pacioli veröffentlichte 1509 ein bis heute bedeutendes Buch über den goldenen Schnitt “De Divina Proportione” (dt. ‘Von der göttlichen Proportion’), für das Leonardo Illustrationen anfertigte. Das Buch enthält unter anderem eine Übersetzung von Vitruvs Beschreibung der menschlichen Proportionen, die Leonardo zu der berühmten Zeichnung des Vitruvianischen Menschen inspirierte.
Besonders bemerkenswert ist, dass Pacioli im Anhang seines Buches eine Typographie auf der Grundlage der Geometrie vorschlug. Er empfahl, dass die Gestaltung der Buchstaben den bekannten Proportionen der klassischen Geometrie folgen sollte, wie etwa Halbierung, Drittelung und Goldener Schnitt. Paciolis Vorschläge zur Integration geometrischer Prinzipien in die Typographie hatten eine nachhaltige Wirkung. Seine Gestaltungsregeln sind auch heute noch in Lehrbüchern zur Typographie zu finden.

Der Mathematiker Pacioli war gut mit Leonardo da Vinci bekannt, der das Buch in Teilen illustrierte

Fazit zur Verwendung des goldenen Schnitts in der Kunst
Der goldene Schnitt wird in der Kunst überall da eingesetzt, wo etwas unterteilt werden soll. Neben den hier gezeigten Beispielen kann er z.B. die Länge eines Films unterteilen, um bestimmte Szenen oder Einstellungen hervorzuheben. In der Musik kann z.B. die Anzahl bestimmter Takte zueinander im goldenen Schnitt stehen oder die Frequenz bestimmter Töne (etwa die Töne C und Gis). In der Dichtung kann die Anzahl der Silben der Zeilen wichtige Inhalte betonen, z.B. durch die Verwendung der Fibonacci Zahlen 3, 5, und 8 für die Anzahl der Buchstaben aufeinanderfolgender Wörter oder der Anzahl der Silben drei aufeinanderfolgender Zeilen.
Der goldene Schnitt wird in der Kunst selten allein eingesetzt, sondern fast immer im Zusammenspiel mit anderen häufig verwendeten Proportionen wie Halbierung, Drittelung und Viertelung. Das Zusammenspiel der Proportionen so zu gestalten, dass das Gesamte zum einen harmonisch wirkt und zum anderen die jeweilige Idee des Kunstwerks unterstreicht, ist eine hohe Kunst und erfordert ein gewisses Maß an Verständnis von Geometrie, sowie die Fähigkeit durch sie eine Erzählung auszudrücken. Weil der goldene Schnitt aus mathematischer Sicht die schönste Proportion ist, betont er meistens eine oder mehrere Besonderheiten eines Kunstwerks.
Umgekehrt heißt das jedoch nicht, dass nur das Kunst ist, was den goldenen Schnitt verwendet bzw. auf andere Art besonders harmonisch proportioniert ist.
Geometrische Konstruktion
1
1
2
3
5
8
13
21
34
55
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
1
9
36
84
126
126
84
36
9
1
V Goldener Schnitt nach Euklid
Es gibt verschiedene Methoden den goldenen Schnitt zu konstruieren. Die bekannteste ist die des antiken Mathematikers Euklid (3. Jahrhundert v. Chr).
- Konstruktion eines Rechtecks aus zwei nebeneinanderliegenden Quadraten über der zu teilenden Strecke AB (der Übersichtlichkeit wegen wurde hier auf die Konstruktion ders Rechtecks verzichtet)
- Einzeichnen der Diagonale des Rechtecks
- Abtragen der Seitenlänge eines Quadrats auf der Diagonalen
- der andere Teil der Diagonale wird auf die ursprünglich gegebene Strecke übertragen (hellblaue Linie)
- dieser teilt die ursprüngliche Strecke im Verhältnis des goldenen Schnitts (gelber Punkt)
Das goldene Rechteck
Wird der Minor um 90° gedreht, entsteht ein goldenes Rechteck, das heißt die Seitenlängen stehen im Verhältnis des goldenen Schnitts (Mouseover, oranges Rechteck).
VI Goldener Schnitt nach George Odom
George Odom (1941-2010) war ein US-amerikanischer Künstler und Mathematiker, der sich mit Geometrie und vor allem dem Goldenen Schnitt beschäftigt hat. Am bekanntesten ist die 1982 von ihm entdeckte Methode den goldenen Schnitt mit Hilfe eines gleichseitigen Dreiecks zu konstruieren. Die Lösung ist aus mathematischer Sicht sehr schön, weil sie einfach ist (Mouseover).
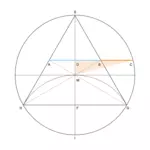
- In einem gegebenen Kreis wird der Durchmesser und seine Mittelhalbierende eingezeichnet
- Konstruktion eines gleichseitigen Dreiecks in den Kreis
- der Schnittpunkt I der Mittelhalbierenden des Durchmessers ist der Mittelpunkt eines Kreises mit demselben Radius wie der des gegebenen Kreises (Kreisbogen durch H und G)
- die Schnittpunkte beider Kreise bilden die Basis des gleichseitigen Dreiecks (H und G)
- von diesen Schnittpunkten wird die Basis auf dem ersten Kreis abgetragen, so dass ein gleichseitiges Dreieck entsteht (EHG)
- von zwei Eckpunkten des Dreiecks wird je eine Gerade durch den Mittelpunkt des Umkreises gezogen (Winkelhalbierende, bzw. Mittelsenkrechte der gegenüberliegenden Seite (hier HB und AG)
- die Schnittpunkte der zwei Geraden mit den Seiten des Dreiecks werden verbunden (A und B), und in eine Richtung verlängert, so dass sie den Umkreis schneiden (C)
- Die Strecken AB und AC bzw. BC und AB stehen im Verhältnis des goldenen Schnitts
Mathematischer Nachweis des Goldenen Schnitts in Odoms Konstruktion
Grundidee ist die Berechnung der Länge der Strecke DB bzw. DC über den Satz des Pythagoras für das Dreieck DMC (orange Fläche). Dazu wird die Länge des Radius des Umkreises mit 1 bestimmt (Einheitskreis).
- MC entspricht dem Radius des Umkreises und ist 1 lang
- DC setzt sich zusammen aus DB und BC
- DB ist nach dem Strahlensatz für die Strahlen EF und EG halb so groß wie FG, da EB halb so groß ist wie EG
- FG ist der Sinus von 60°, also ~0,866, DB damit sin(60°)/2 = ~0,433
- BC bleibt vorerst unbekannt
- DM lässt sich über den Satz des Pythagoras für das Dreieck BDM berechnen
- DM = BM2 - DB2
- BM ergibt sich aus der Höhe HB des gleichseitigen Dreiecks von der der Radius HM des Umkreises abgezogen wird.
Die Formel für die Berechnung der Höhe im gleichseitigen Dreieck lautet:
h = Seitenlänge/2 * 3
Die Seitenlänge HG ist das doppelte der bereits bekannten Länge FG (Symmetrie). Durch Einsetzen ergibt sich:
h = HB = (2 * sin(60°)) / 2 * 3 = 1,5
BM = HB - HM = 1,5 - 1 = 0,5 - DB ist bereits bekannt: sin(60°)/2
- durch Umstellen nach DM und Einsetzen:
DM =0,52 - (sin(60°)/2)2 = 0,25 - 0,1875 = 1/4
Da nun alle Seitenlängen für das Dreieck DMC bekannt sind (außer die Teilstrecke BC), kann auch hier der Satz des Pythagoras angewendet werden, um BC zu erhalten. Durch Umstellen und Einsetzen ergibt sich:
MC2 = DM2 + (DB + BC)2 | -DM2, Wurzel ziehen, -DB
MC2 - DM2 - DB = BC
12 - 1/42 - sin(60°)/2 = BC
BC = 12 - 1/42 - sin(60°)/2 = ~0,535
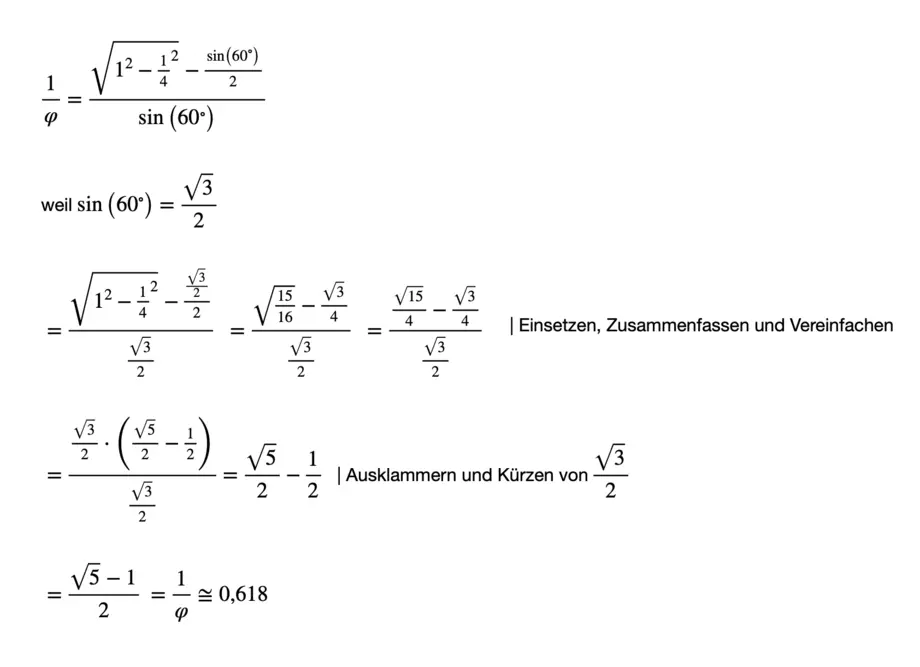
Schließlich der rechnerische Nachweis, dass BC und AB zueinander im Verhältnis des goldenen Schnitts stehen:
1/φ = BC / AB = ~0,618
Die Länge AB ist bekannt, denn aufgrund der Symmetrie des gleichseitigen Dreiecks EHG ist AB das Doppelte von
DB = sin(60°)/2,
so dass AB = sin(60°)/2*2 = sin(60°).
Durch Einsetzen von BC / AB entsteht:
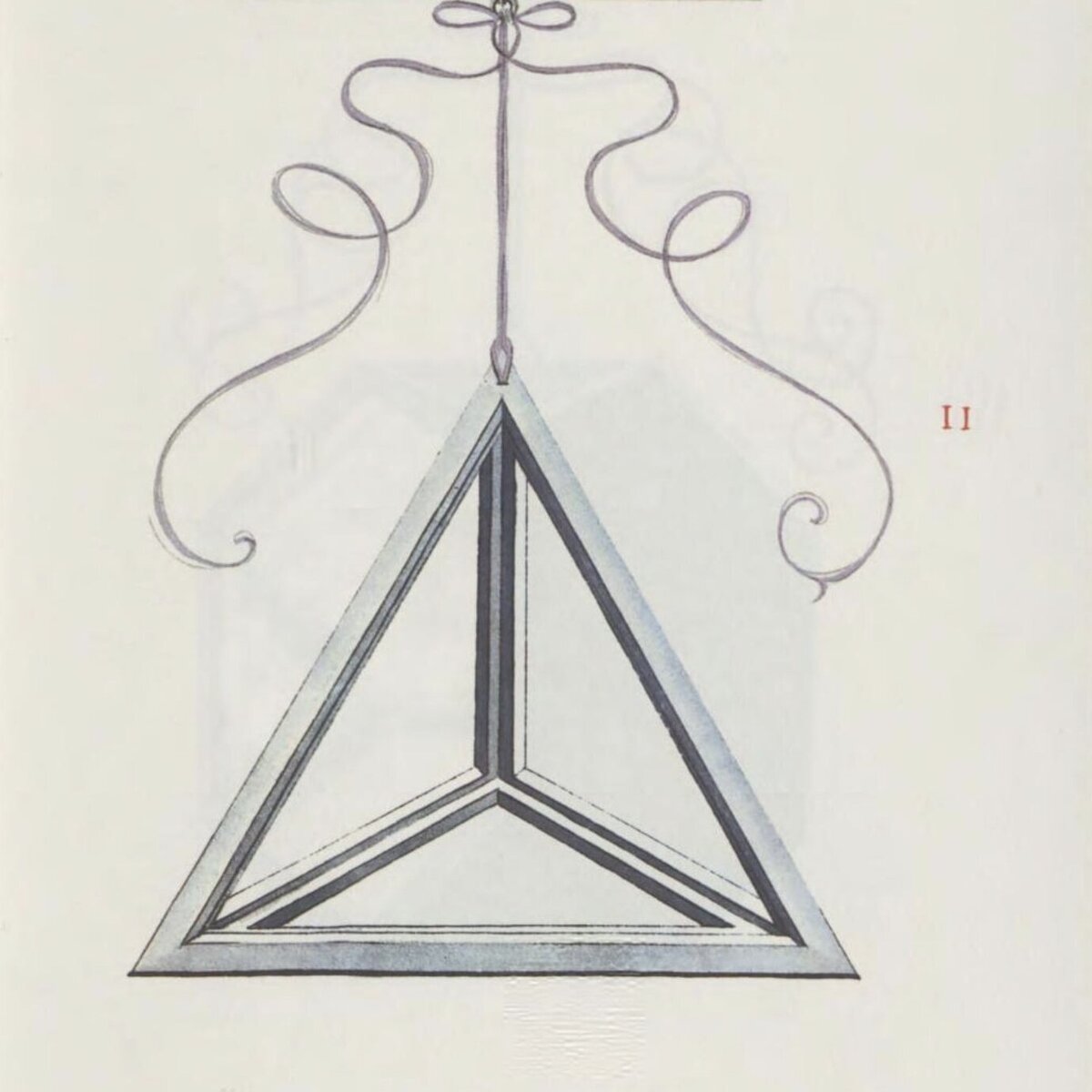
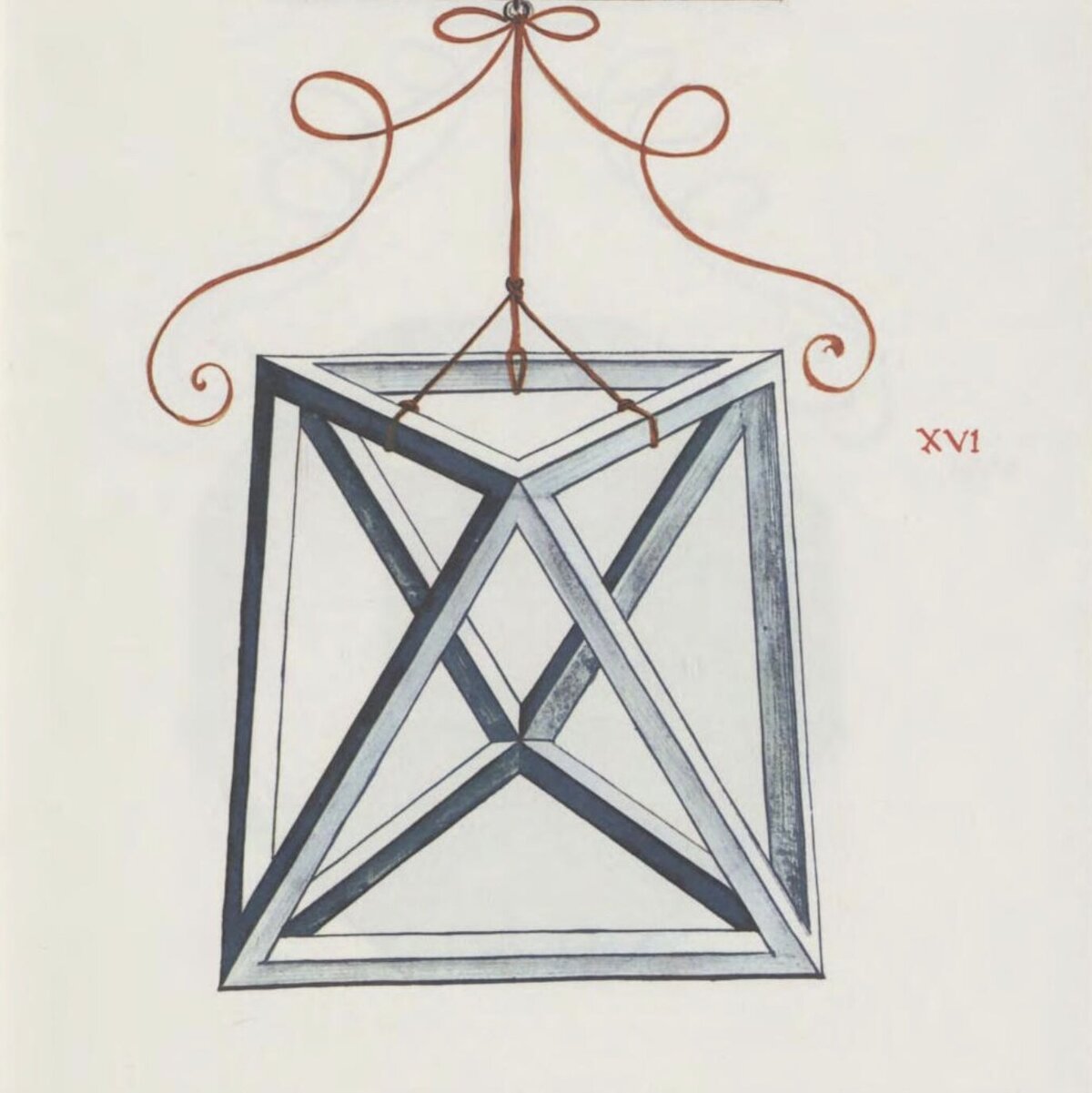
VII Regelmäßiges Fünfeck
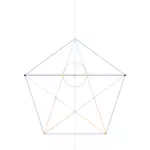
Der goldene Schnitt ist notwendig, um ein regelmäßiges Fünfeck zu konstruieren. In einem regelmäßigen Fünfeck sind alle Seiten gleich lang.
Gegeben ist eine Strecke AB, die im goldenen Schnitt geteilt wurde (Punkt D). Ebenso ist die Mittelsenkrechte der Strecke notwendig (gestrichelte Vertikale durch den Punkt M, der Übersichtlichkeit wegen wurde hier auf die Konstruktion der Mittelsenkrechten verzichtet).
Linker und rechter Eckpunkt des Fünfecks
- entsprechen den Eckpunkten der gegebene Strecke AB
Oberer Eckpunkt
- der Minor DB des goldenen Schnitts der gegebenen Strecke wird als Radius eines Kreises um D bestimmt. mit diesem Radius wird um D ein Kreis gezogen. Da wo er auf die Mittelsenkrechte der Strecke AB trifft, befindet sich der obere Eckpunkt des 5-Ecks (oberer blauer Punkt)
Rechter unterer Eckpunkt
- vom oberen Eckpunkt des 5-Ecks wird eine Linie durch den goldenen Schnitt von AB gezogen, also durch den Punkt D. Die Länge der Strecke AB wird auf diese Linie abgetragen. Es ergibt sich der rechte untere Eckpunkt F
Linker unterer Eckpunkt
- Um den Mittelpunkt M der gegebenen Strecke AB wird ein Kreis gezeichnet, dessen Radius so lang ist, wie der Abstand vom goldenen Schnitt D und dem Mittelpunkt M. Im linken Schnittpunkt dieses Kreises mit der gegebenen Strecke AB entsteht der Punkt C.
- Vom oberen Eckpunkt E des 5-Ecks wird eine Linie durch C gezogen. Die Länge der Strecke AB wird auf diese Linie abgetragen. Es ergibt sich der linke untere Eckpunkt G
Werden die fünf Eckpunkte miteinander verbunden, entsteht ein regelmäßiges 5-Eck (dunkelblaue Linien). Die fünf Diagonalen des 5-Ecks bilden einen fünfzackigen Stern. Diese Linien schneiden sich stets im goldenen Schnitt (hellblaue und orange Linien).


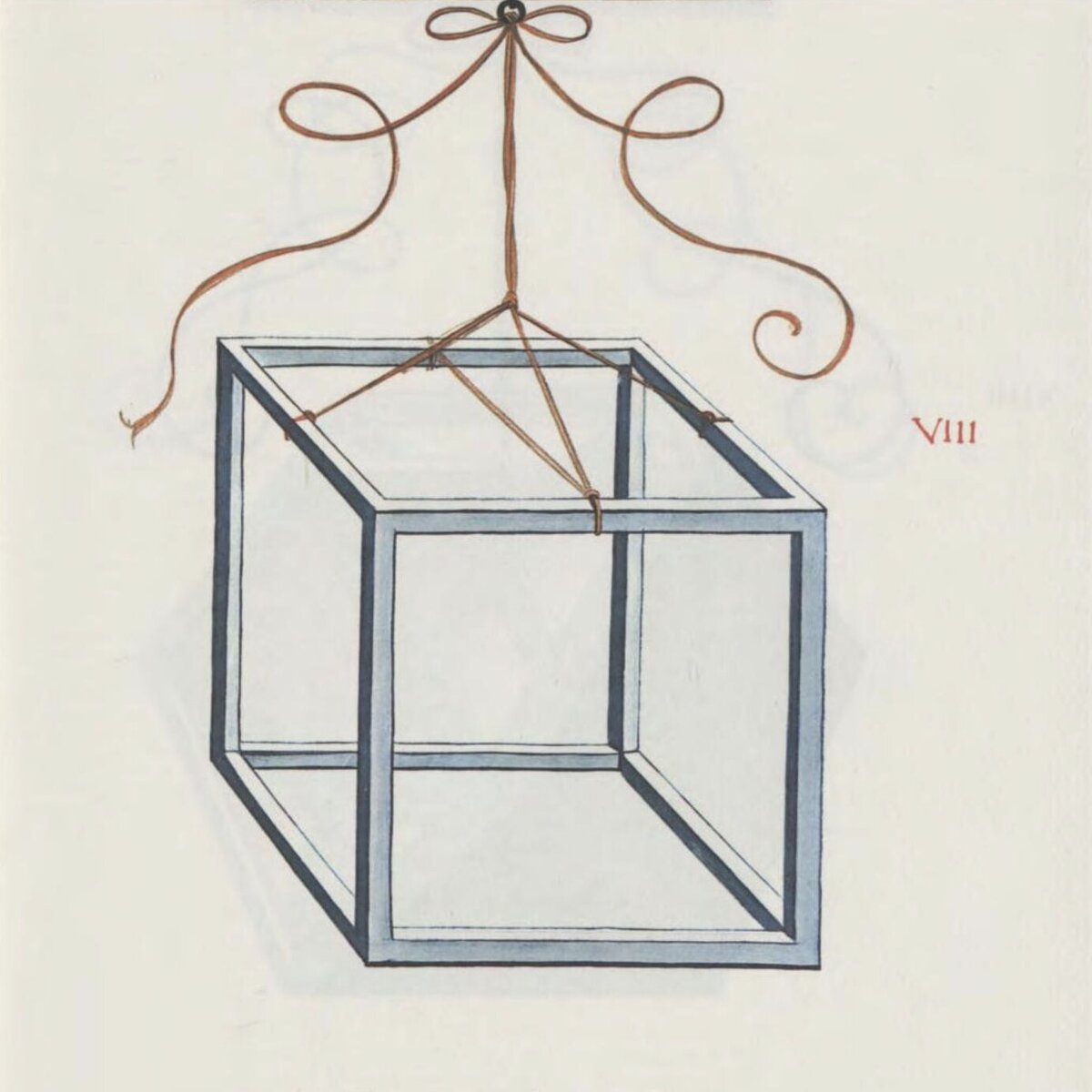
VIII Goldene Spirale
Die goldene Spirale wird häufig in einer Annäherungskonstruktion dargestellt.
- Einzeichnen einer Strecke (unterste Horizontale)
- Teilen der Strecke im goldenen Schnitt (blau: goldener Schnitt Major, orange: goldener Schnitt Minor)
- vom goldenen Schnitt der Strecke wird ein 90° Winkel im Uhrzeigersinn gezogen. Die Länge der Strecke muss dem goldenen Schnitt Major der Ausgangsstrecke entsprechen
- diese Strecke wird nun ebenfalls im goldenen Schnitt geteilt, dabei muss der goldene Schnitt Minor am goldenen Schnitt der ersten Strecke anliegen (orange Linien)
- der Vorgang wird unendlich wiederholt (hier noch weitere sechsmal)
- in jedes der Quadrate wird ein Viertelkreis gezeichnet, so dass sich die Viertelkreise berühren
- Einzeichnen der zwei Diagonalen zur Bestimmung des Mittelpunktes der Spirale (Mouseover/Tap)

Die goldene Zahl
Die goldene Zahl gibt das Teilungsverhältnis des goldenen Schnitts an. Sie wird meist mit dem 21. griechischen Buchstaben φ (Phi) bezeichnet und hat den gerundeten Wert von 1,618. Die goldene Zahl ist eine irrationale Zahl und damit unendlich. Sie entsteht durch Addieren der Länge des Majors einer im goldenen Schnitt geteilten Strecke der Länge 1 und der Zahl 1, also ~0,618 + 1 = ~1,618.
Berechnung der goldenen Zahl
Der Zahlwert der goldenen Zahl ergibt sich aus der geometrischen Konstruktion des goldenen Schnitts nach Euklid und hat dort die Länge der Strecke AE (Abbildung links). Diese Länge kann mit dem Satz des Pythagoras berechnet werden, denn die Punkte ABC formen ein rechtwinklinges Dreieck.
Die Länge der Strecken AB und BC sind bekannt, da das Rechteck aus zwei nebeneinanderliegenden Quadraten besteht. Damit ist die Höhe des Rechtecks genau halb so hoch, wie es breit ist. Hier hat das Rechteck die Breite von 1, daher ist es 0,5 hoch.
Die Länge der Diagonale AC ergibt sich aus dem Satz des Pythagoras:
AC2 = AB2 + BC2
AC = 12 + 0,52 = 1,25 = ~1,18
Die Länge der goldenen Schnitts ergibt sich durch Abtragen der Strecke AD auf AB.
Die Länge der Strecke AD ist bekannt durch AD = AC - DC, denn DC ist wie BC der Radius des Kreises um C und hat daher die Länge von 0,5.
Die Länge von AD und damit des goldenen Schnitts beträgt also:
1/φ = AC - DC = ~1,18 - 0,5 = ~0,618
Variante mit der Wurzel aus 5
Verwirrenderweise wird die Breite des Rechtecks häufig nicht mit 1, sondern mit 2 angegeben. Dadurch verändert sich auch die Höhe des Rechtecks von 0,5 zu 1. Dieselbe Rechnung mit den neuen Werten:
AC = 22 +12 = 5
AD = 5 - 1 = ~1,236
Um auf das ursprüngliche Zahlenverhältnis des goldenen Schnitts für ein Rechteck mit der Breite von 1 zu kommen, muss dieser Wert durch 2 dividiert werden (Mouseover/Tap). Zwar teilt die Strecke AE die Strecke AB im goldenen Schnitt, jedoch hat diese die Länge 2 und gesucht ist der goldene Schnitt der Länge 1. Folglich muss AE im Punkt M geteilt werden, was zu der gesuchten Größe von 0,618 führt (Mouseover/Tap, gelber Punkt). Rechnerisch ergibt sich folgendes:
AD = (5- 1) / 2 = ~0,618
Aus der geometrischen Überlegung heraus ist offensichtlich, dass diese Methode einen Schritt mehr benötigt. Dass sie dennoch die populärere Variante ist, kann nur dadurch erklärt werden, dass
1/φ = (5 - 1) / 2 angenehmer zu lesen ist, als
1/φ = 1,25 - 0,5 aus der vorherigen Rechnung
Darstellung der goldenen Zahl auf einem Zahlenstrahl von 0 bis 3. Es ist gut zu erkennen, dass φ sich aus 1 und dem Wert des goldenen Schnitts von 1 ergibt, der ungefähr bei 0,618 liegt.
Fibonacci Folge und Pascalsches Dreieck
1
1
2
3
5
8
13
21
34
55
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
1
9
36
84
126
126
84
36
9
1
IX Die Fibonacci Folge
Die Fibonacci Folge ist nach dem italienischen Mathematiker Leonardo Fibonacci (um 1170-1240) benannt. Die Zahlenfolge ergibt sich, wenn die letzten zwei bekannten Zahlen der Folge miteinander addiert werden und diese Summe der Folge hinzugefügt wird, beginnend mit Null und Eins.

Die Fibonacci Folge steht im unmittelbaren Zusammenhang zum Goldenen Schnitt, da das Ergebnis der Division zwei aufeinanderfolgender Zahlen dieser Reihe sich stetig dem Teilungsverhältnis des Goldenen Schnitts ~0,618 annähert.
| Rechnung | Fibonacci Folge | Teilungsverhältnis |
| – | 0,1 | 0/1 = 0 |
| 0 + 1 = 1 | 0,1,1 | 1/1 = 1 |
| 1 + 1 = 2 | 0,1,1,2 | 1/2 = 0,5 |
| 1 + 2 = 3 | 0,1,1,2,3 | 2/3 ≈ 0,666 |
| 2 + 3 = 5 | 0,1,1,2,3,5 | 3/5 = 0,6 |
| 3 + 5 = 8 | 0,1,1,2,3,5,8 | 5/8 = 0,625 |
| 5 + 8 = 13 | 0,1,1,2,3,5,8,13 | 8/13 ≈ 0,615 |
| ... | ||
| 89 + 144 = 233 | 0,1,1,...,144,233 | 144/233 ≈ 0,6180 |
X Pascalsches Dreieck
Die Bezeichnung Pascalsches Dreieck geht auf den Naturwissenschaftler Blaise Pascal zurück (1623-1662).
Zentrierte Darstellung
Dabei ergeben sich die Zahlen des Dreiecks derart, dass jede Zahl die Summe der zwei darüberliegenden Zahlen ist. Gibt es nur eine Zahl, ist die andere 0 (für die Zahlen am äußeren Rand des Dreiecks). Begonnen wird an der oberen Spitze des Dreiecks mit dem Setzen der Zahl 1.
Das Pascalsche Dreieck wurde in der zentrierten Darstellung hauptsächlich dazu benutzt, beliebige Potenzen von Binomen aufzulösen, z.B.
(a+b)2 = 1a2 + 2a1b1 + 1b2
1, 2 und 1 entsprechen den Zahlen der dritten Reihe des Pascalschen Dreiecks. Die Zahlen der darauffolgenden vierten Reihe (1,3,3,1) können für das Auflösen der dritten Potenz des Binoms (a+b) verwendet werden, also für
(a+b)3 = 1a3 + 3a2b1 + 3a1b2 + 1b3
usw.
Linksbündige Darstellung
Das Pascalsche Dreieck kann auch linksbündig dargestellt werden (Mouseover). Dadurch werden die darin enthaltenen Zahlenfolgen besser ablesbar.
2. Spalte: die natürlichen Zahlen
3. Spalte: die Dreieckszahlen
4. Spalte: die Tetraederzahlen
Die Fibonaci Folge im Pascalschen Dreieck
Die Fibonacci Zahlenfolge ergibt sich aus der Summe der Zahlen, die auf einer Diagonale von 45° liegen, wenn das Dreieck linksbündig dargestellt wird (Mouseover/Tap).
Das größte Vergnügen ist die Erkenntnis
Downloads
Nobody is perfect - das gilt auch für nicofranz.art!
Alle Hinweise zu Fehlern und Korrekturen nehmen wir mit Dank entgegen. Solltest Du inhaltliche Fehler auf dieser Seite finden, lass es uns gerne wissen.