The golden ratio
What is the golden ratio?
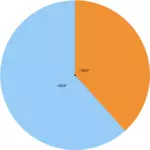
The golden ratio is a ratio used in mathematics, architecture, art and science. It describes the ratio between two sizes in which the smaller part is in the same proportion to the larger part as the larger part is to the whole. The division ratio is denoted by the Greek letter φ (Phi) and has the rounded value of 1.618 (or 1/φ = ~0.618).
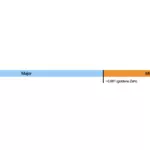
A distance of length 1 is divided by the golden ratio rounded at 0.618. The larger part of the resulting two parts is called the major and the smaller part the minor. The difference between the golden ratio and other known division ratios becomes clearer in comparison. Here using the example of halving and thirds.
A section of length 1 is divided in half at 0.5. The resulting two parts are called halves.
A section of length 1 divides into thirds at ~0.33 and ~0.66. The resulting three parts are called thirds.
Why is it called the "golden" ratio?
The name "golden ratio" refers to the fact that this division ratio is considered particularly harmonious and aesthetic in mathematics. Additionally, the golden ratio is commonly found in architecture, art, and nature, which contributes to its perception as something "golden" or "ideal." Alternative names for it include the "divine ratio," "Fibonacci ratio," or "divine proportion" (Italian: 'Divina proportione').
Where does the golden ratio occur?
The golden ratio appears in many areas of nature and art.
- In biology, the golden ratio can be found in the form of plants and animals, such as the arrangement of leaves on a branch or human proportions
- In mathematics, the golden ratio is an essential component of the Fibonacci sequence
- In painting and photography, it is used to balance and make compositions more interesting
- In architecture, it is often employed to design proportions of buildings and interiors.
There are many other examples of the occurrence of the golden ratio. It is often considered aesthetically pleasing and harmonious.
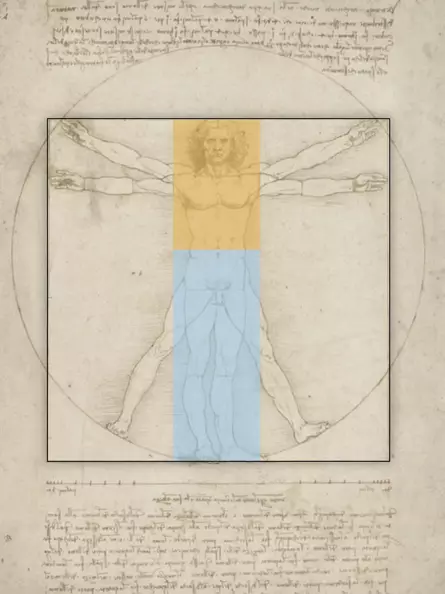
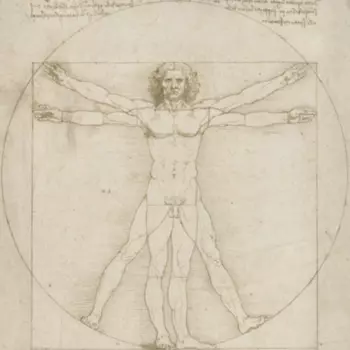
The golden ratio can also be found in human proportions, with the navel roughly located at the height of the golden section of the body's height
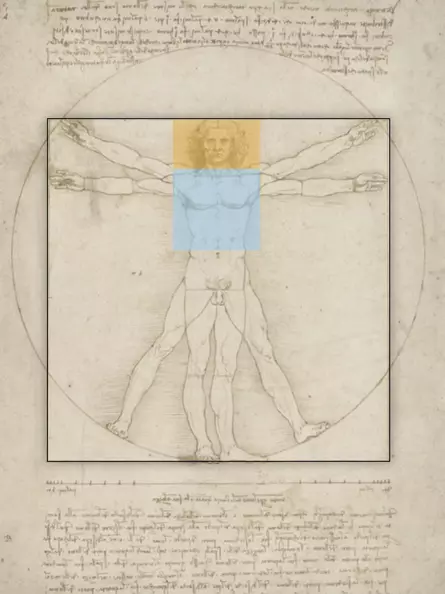
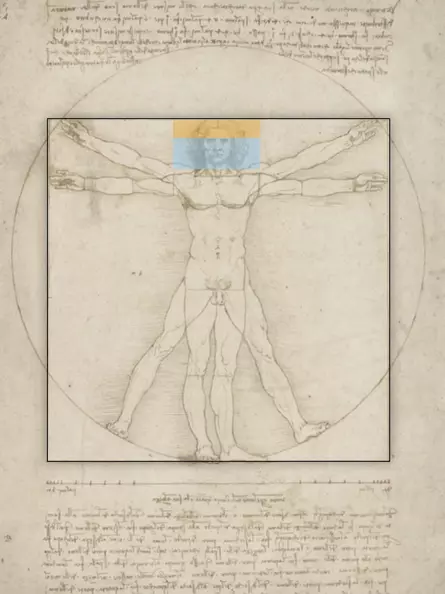
Geometry holds two great treasures: one is the Pythagorean Theorem, the other is the Golden Section. The first we can compare to a bushel of gold, the second we can call a precious jewel.
Golden Ratio and Proportion
A proportion is the size ratio of two parts. The uniqueness of the Golden Ratio's proportion can be well demonstrated when compared to other size ratios. To illustrate this, the Golden Ratio is compared to halving and quartering, two other commonly used proportions.
Halving
When a segment of 1 is divided exactly in the middle, two equal parts are created. Each of the two parts is exactly half the length of the original segment, measuring 0.5 each (black/gray stripes).
Golden Ratio
What's special about the Golden Ratio is that the size ratio of the smaller part to the larger part is the same as that of the larger part to the original segment. This means the orange part relates to the blue part in the same way that the blue part relates to the sum of blue and orange.
Mathematically, it results in: Blue: ~0.618 Orange: 1 - 0.618 = ~0.382 Orange to Blue: 0.382 / 0.618 = 0.618 Blue to Black: 0.618 / 1 = 0.618
So, Orange to Blue and Blue to Black have the same proportion to each other.
Proportion of Infinity
The division in the Golden Ratio can be continued infinitely. Each part then maintains the same proportion to its parts. Therefore, it can also be said that the Golden Ratio is the proportion of infinity.
Instead of dividing the segment, it's also possible to enlarge it. In this case, it should be multiplied by 1 + 0.618 = 1.618. This results in a larger whole, with its parts appearing harmonious to each other because they share the same proportion. This only happens with division in the Golden Ratio.
Quartering
To illustrate another proportion frequently used in architecture, the quartering is considered (red/green stripes).
When a segment is divided into quarters, the calculations are as follows: Red: ~0.25 (1/4) Green: 1 - 0.25 = 0.75 (3/4) Red to Green: 0.25 / 0.75 = 0.33333 (1/3) Green to Black: 0.75 / 1 = 0.75 (3/4)
As with halving, the parts here do not share the same size ratio with each other as the larger part does with the whole.
Variations of the Golden Ratio
Golden Rectangle
In a golden rectangle, the side lengths are in the Golden Ratio proportion. It is formed when the minor side of a Golden Ratio is rotated by 90 degrees.
A golden rectangle can always be divided into a square and a smaller golden rectangle (Mouseover/Tap).
Golden Spiral
A golden spiral is formed when the radius of a circle decreases by a factor of the Golden Ratio every 90 degrees of rotation around its center (Mouseover/Tap). Therefore, it is always bounded by a golden rectangle.
A common approximation construction involves repeatedly dividing a golden rectangle into smaller golden rectangles. Within the resulting squares, a quarter circle is drawn in a way that continues an existing quarter circle (yellow curve).
All golden rectangles share only two diagonals (dashed lines). Their intersection point is the center of the spiral. The spiral can also be drawn from the center outward, continually increasing in size.
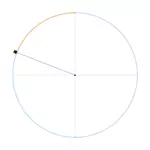
Golden Angle
The Golden Ratio can be applied not only to line segments but also to the circle. The golden angle is formed when a full circle of 360° is multiplied by the Golden Ratio. This results in two angles: 360° * 0.618 = ~222.5° and 360° - ~222.5° = ~137.5°. The smaller of the two angles is referred to as the golden angle (orange). Not only the angles but also the lengths of the resulting circular arcs are in the Golden Ratio to each other (Mouseover/Tap).
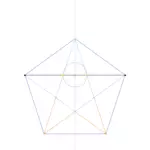
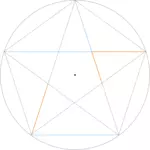
Pentagon, Pentagram, and Golden Triangles
Pentagon (from Ancient Greek 'Five (corner) angles') is the Greek term for a five-sided figure. However, it usually refers to a regular pentagon, meaning one in which all sides are of equal length.
When the vertices are connected by diagonals, a pentagram (from Ancient Greek 'Five lines') is formed, also known as a five-pointed star.
Key Angles
Especially in the composition of paintings, the angles of the regular pentagon are frequently used:
- 72°, the central angle of the pentagon
- 108°, the interior angle of the pentagon (on the right) and the exterior angle between the points of the pentagram (on the left)
- 36°, the interior angle of the pentagram's point
Golden Triangles
Golden triangles are formed within a regular pentagon. These are isosceles triangles in which the lengths of two sides are in the Golden Ratio to each other. There can be exactly two variations (Mouseover/Tap).
- Interior Angle Variation 1 (blue triangle): 36°, 72°, and 72°
- Interior Angle Variation 2 (orange triangle): 108°, 36°, and 36°
Myth of the Pentagon
A regular pentagon can only be constructed with an understanding of the Golden Ratio. In classical geometry, only a compass and an unmarked straightedge are allowed for this purpose.
In antiquity and the Middle Ages, the construction of a regular pentagon, and thus the Golden Ratio, was known to only a few. Pentagons were therefore considered mystical symbols for a long time, accessible only to those with access to books and knowledge.
[Translate to English:] Ikosaeder (Platonischer Körper)
[Translate to English:]
Ein Ikosaeder ist einer der fünf platonischen Körper. Es gehört zu den regelmäßigen Polyedern (Vielecken), denn es besteht aus 20 gleichseitigen Dreiecken. Jeweils fünf dieser Dreiecke berühren sich in einen gemeinsamen Punkt. Dadurch bilden sie regelmäßige 5-Ecke (orange Linien, Mouseover).
Ein weiterer Zusammenhang mit dem goldenen Schnitt besteht in seiner inneren Struktur, d.h. den Strecken zwischen den voneinander entferntesten gegenüberliegenden Ecken. Denn ein Ikosaeder wird aus drei goldenen Rechtecken gebildet, die so in einen Raum gelegt werden, dass je eines nach der x-, y- und der z-Achse ausgerichtet ist, wobei ihr Schwerpunkt in einem gemeinsamen Punkt liegt (gelber Punkt in rotem, grünem und blauem Rechteck). Die Ecken der goldenen Rechtecke werden verbunden (hellblaue Linien).
Beispiele
Ein Ikosaeder kommt in der Natur häufig vor, da es von allen regelmäßigen Polyedern mit gegebenem Durchmesser das größte Volumen besitzt
- Proteinhüllen von Viren (Kapside) haben meist die Form eines Ikosaeders
- das chemische Element Bor kann in Form von Borclustern auftreten. 12 Boratome können ein solches Cluster bilden (B12), das dann die Form eines Ikosaeders annimmt
- das Mineral Pyrit kann in der Form eines Ikosaeders entstehen u.v.m.
Examples
1
1
2
3
5
8
13
21
34
55
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
1
9
36
84
126
126
84
36
9
1
I Stock charts and Fibonacci retracement
coming soon
II Mecca and the Golden Ratio of the Poles
Mecca is the birthplace of the Prophet Muhammad and home to the central holiest site in Islam, the Kaaba. The geographical location of Mecca is closely related to the Golden Ratio.
General Explanation of Latitude and Longitude
Every location on Earth can be uniquely specified by latitude and longitude coordinates.
Latitude is determined by imagining a line from the center of the Earth to the equator, with this angle set to zero. The North and South Poles are now situated 90° above or below the equator (northern or southern latitude).
For longitude, in a top-down view of the Earth, a line is imagined from the North or South Pole to the equator. The angle zero was established as the Prime Meridian in 1884 and passes through Greenwich, England. Now, every location on Earth is situated up to 180° east or west of this point.
Since the Prime Meridian was arbitrarily chosen and could just as easily pass through Tokyo or San Francisco, longitude is not relevant in the context of Mecca's geographical position. However, latitude, which has natural reference points in the Earth's North and South Poles, is significant.
The Geographic Latitude of Mecca
Mecca is located at 21.25° north latitude (green line). The distance of 1 degree of latitude on the Earth's surface is constant and approximately 111.7 kilometers.
The distance from Mecca to the South Pole (blue point) is:
(90° + 21.25°) * 111.7 km = 12,426.63 km (blue line)
The distance from Mecca to the North Pole (orange point) is:
(90° - 21.25°) * 111.7 km = 7,679.38 km (orange line)
Both distances are in the ratio of the Golden Ratio:
7,679.38 km / 12,426.63 km = ~ 0.618.
III Blossoms and the Golden Angle
The Spirals of the Golden Angle and the Fibonacci Sequence
Around a central point, an angle of 137.5° is drawn. The point is marked. Starting from this point, the angle is drawn again from the center, and so on. With each new angle drawn, the radius is extended by a very short distance.
The numbers 8, 13, and 21 are part of the Fibonacci sequence. When every 8th, 13th, or 21st angle is marked, these markings create a spiral pattern. The spiral pattern occurs only with Fibonacci numbers




Occurrences in Nature
All members of the Asteraceae family exhibit the Golden Angle. The spirals are clearly visible in the flowers. Such an arrangement of petals ensures that even densely packed petals receive the maximum possible exposure area for light (Mouseover/Tap).
Some examples of Asteraceae include sunflowers, chrysanthemums, chamomile, dandelions, and lettuce.

The central flower head exhibits the spiral pattern of the golden angle

The petals form the spiral of the golden angle
The Golden Ratio in Art
It is important to mention that the Golden Ratio is just one of many proportions used in art, albeit considered one of the most aesthetically pleasing from a mathematical perspective. In addition to the Golden Ratio, various other proportions like thirds, quarters, and more are often used, sometimes within the same artwork. The goal is to maintain the viewer's interest by creating a diverse and engaging composition.
The Golden Ratio in Painting
The Golden Ratio has been used in paintings since the Middle Ages, especially in the composition of images, such as the arrangement of figures. The renowned painter Leonardo da Vinci, considered one of the greatest artists of all time, created some of the most impressive compositions, and it's no wonder that he incorporated the Golden Ratio into his paintings. It's often said that the Golden Ratio was primarily used by Renaissance painters like Leonardo, Raphael, or Albrecht Dürer. However, the presence of the Golden Ratio can be observed throughout various artistic epochs as a part of the composition in the works of outstanding artists. This demonstrates that their paintings were not only inspired by divine intuition but also the product of mathematically inclined individuals.

The painting is structured as a golden rectangle. The Golden Ratio connects the eyes of the Madonna (long diagonal of the golden spiral), the infant John on the left (Golden Ratio of the painting's height), and the infant Jesus on the right (golden spiral)

The Golden Ratio divides the painting vertically, running at the height of the background columns' feet. The major axis is once again divided by the Golden Ratio, passing through Mona Lisa's eyes, with her left eye also precisely at the center of the image (red line)

The left end of the scroll forms a golden spiral

Explanation of the five upper horizontal lines from top to bottom:
Line 1: The hand of God touches Adam at the golden section of the image width (left orange vertical)
Line 2: Division of the major axis of Line 1 in the golden section runs directly next to the left eye of the female angel (right orange vertical)
Line 3: Halving of the minor axis of Line 2 runs through the left eye of the angel on the right edge of the image (right white vertical)
Line 4: Halving of the major axis of Line 2 runs through the left eye of God (left white vertical)
Line 5: Thirding of the minor axis of Line 1 leads to the right eye of Adam (green vertical)
In terms of the image height, the use of classical geometric proportions can also be demonstrated (mouseover). Explanation of the four vertical lines from left to right:
Line 1: The eye of God is located at 1/4 of the image height (lower white horizontal)
Line 2: The left eye of the angel on the right edge of the image is at 1/3 of the image height (green horizontal)
Line 3: The right eye of Adam is at the golden section of the image height (orange horizontal)
Line 4: The eye of the female angel is at 5/12 of the minor axis of Line 3 (upper white horizontal)
The proportion 5/12 is an essential construction feature of St. Peter's Basilica. There, it defines the aspect ratio of the foundation among the characteristic structures (see Leonardo Architecture).

Masaccio's fresco is considered one of the first paintings to accurately depict linear perspective. It is enclosed within a golden rectangle. When the height of this rectangle is divided in the Golden Ratio, it leads to the capitals of the columns in the front arch (upper orange horizontal line). The Golden Ratio of the height of these columns leads to the capitals of the rear arch (lower orange horizontal line). The crossbeam of the central cross is positioned at the Golden Ratio of the height of the front arch (Mouseover/Tap)

Manet is considered one of the pioneers of modern painting.
In the painting, the Golden Ratio of the image width runs through the right eye of the man (orange vertical line). The Golden Ratio is not the only proportion in the painting; for instance, half of the image height aligns precisely along the backrest of the bench (Mouseover/Tap).
Concerning the image height, the Golden Ratio runs along the upper edge of two vases in the background (lower orange horizontal line, blue and beige vase). When the major axis is again divided by the Golden Ratio, it runs through the left eye of the lady (upper orange horizontal line).
The resulting connection between the vase on the left side of the painting and her left eye strongly resembles the Golden Ratio in the Mona Lisa (left column base and left eye). This leads to the conjecture that the two paintings could also be related in terms of their artistic concept, although further investigation is warranted. Every renowned painter has engaged with Leonardo because, among other things, he is still regarded as the most imaginative painter due to his geometric knowledge regarding artistic compositions. It becomes evident that Manet references elements from Leonardo's paintings in another work, "Blonde Woman with Bare Breasts," which serves as a satirical parody of Leonardo's Lady with an Ermine

Rothko was an abstract painter and a pioneer of color field painting.
Conceptually, he divided the painting vertically into 24 units (black/white stripes). The color fields have a distance of 1/24 and 2/24 from the top and bottom, respectively (Mouseover/Tap). Starting from the lower black color field (white horizontal line), the two color fields above it are divided at a height of 13/24 in the Golden Ratio at 5/24 (orange horizontal line). Thus, the upper black color field is 8/24 high (blue). 5, 8, and 13 are Fibonacci numbers
The Golden Ratio in Architecture
The Golden Ratio has been used in architecture since antiquity. Certain pyramids in Egypt are believed to exhibit these proportions, such as the ratio of the slant height to half the base side. However, as the pyramids have significantly deteriorated over time, and their originally thick white limestone casings have been largely removed, it's no longer possible to accurately determine their original dimensions to conclusively prove the use of the Golden Ratio. The oldest confirmed evidence of the Golden Ratio's use in architecture is attributed to the buildings of ancient Greece and Rome.

The Parthenon was built around 450 BC to commemorate the end of the Persian Wars and was dedicated to the protective goddess of Athens, Athena. Shortly after the construction of the temple, the influential philosopher Plato was born in Athens (around 427 BC). In his mathematical writings, he discussed topics such as the Golden Ratio.
The photograph slightly distorts the proportions of the Parthenon's east facade. In essence, the east facade is designed as a golden rectangle, considering the height of the foundation. The reconstructable silhouette of the partially destroyed roof is indicated here with black lines. The roof rests on the capitals of the columns, which are positioned at the Golden Ratio of the building's height.
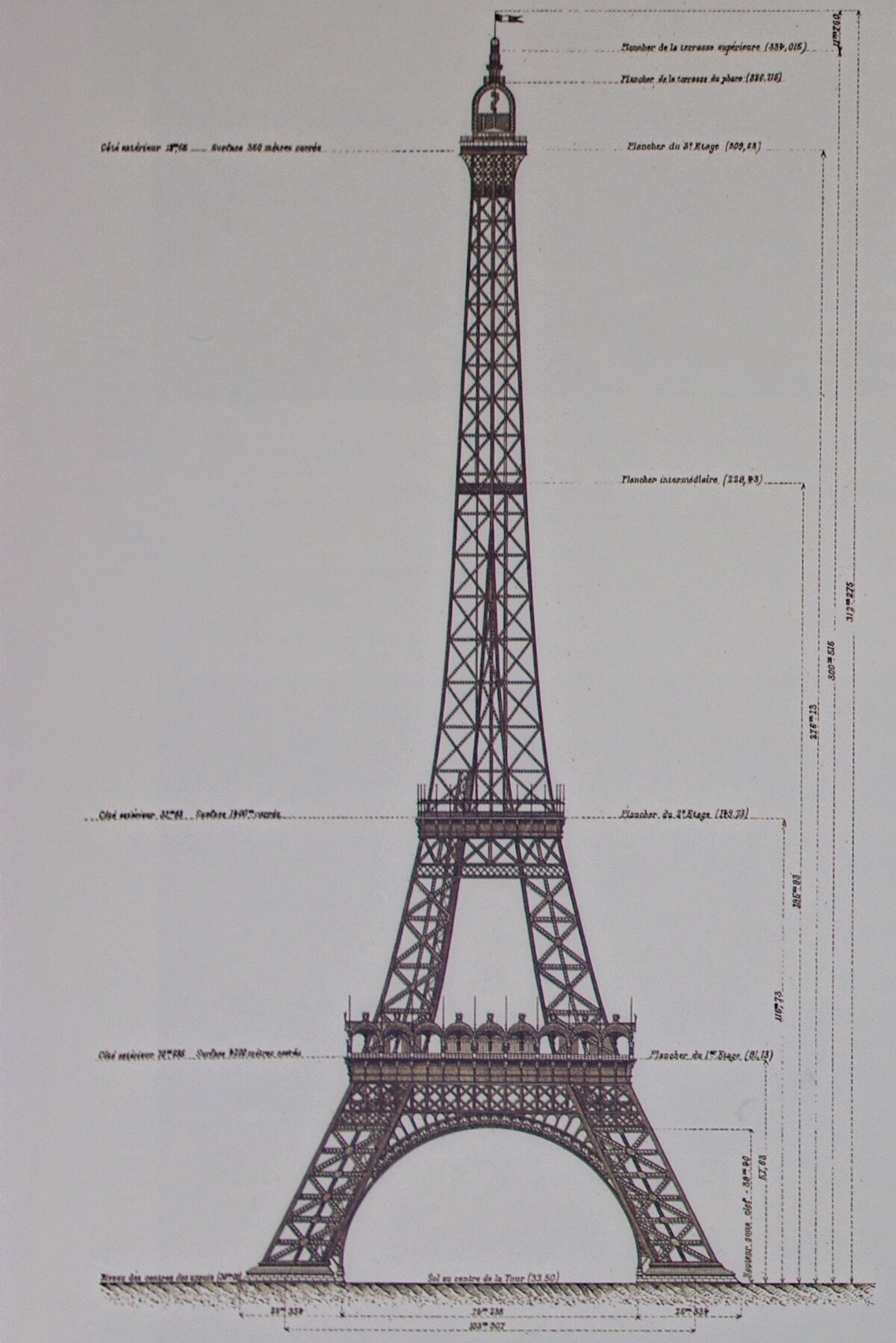
Gustave Eiffel, the chief architect of the tower completed in 1889, presented this to-scale sketch in his 1900 book "La tour de trois cents mètres" (French: 'The Tower of 300 Meters').
- The distance from the foundation to the first platform is the same as from the first platform to the second (right black/white stripe).
- The four pillars of the tower converge at a distinctive ring structure. It marks half the distance from the second platform to the third platform at the tower's pinnacle (left black/white stripe)
- Overall, the height of the tower is divided by the Golden Ratio at the second platform (blue/orange vertical line)
Gustave Eiffel also included proportions in the tower's pinnacle, including specifying the dimensions of the flagpole. However, as the top of the tower has been modernized over time, his original idea has been lost.
It's interesting how Eiffel plays with the circular arch in the lower part of the tower. Its height is nearly in the Golden Ratio with respect to the distance from the foundation to the first platform (green/red stripe). In reality, it's about 2/3, or ~0.666 instead of 0.618.
- Nonetheless, there is still a Golden Ratio present in this area: the sum of the width of the tower's feet is in the Golden Ratio to the diameter of the circular arch (blue/orange horizontal line). When this distance is divided in the middle, two segments side by side are divided in the Golden Ratio (Mouseover/Tap)
- The first platform is the widest, the second platform exactly half the size (black/white horizontals). Based on the sketch, it's uncertain whether the third platform at the top should also be half the size of the second. In this representation, the ratio is only about ~46% (instead of 50%). The same applies to the ratio between the width of the foundation and the first platform, which comes very close to the Golden Ratio at ~0.595 (instead of 0.618)
In conclusion, the Eiffel Tower is a successful example of thoughtful proportioning due to its simple elegance. It has also become evident that the aesthetics of the composition of an artwork are not solely the result of the Golden Ratio but rather arise from the interplay of various proportions.

The front facade forms a golden rectangle.
Around 1947, the building was designed under the leadership of two star architects, Le Corbusier and Oscar Niemeyer.
The French architect Le Corbusier (1887-1965) was a lifelong proponent of the Golden Ratio and developed his own measurement system based on it, known as the Modulor, which he used in many of his famous buildings.
The Brazilian architect Oscar Niemeyer (*1907) was responsible for designing public buildings during the founding of Brasília, the capital of Brazil. He passed away in 2012 at the age of 104
The Golden Ratio in Photography
The division ratio of the golden ratio (0.618 or 1.618) is quite close to another commonly used division ratio, the ratio of 2:3, which is 2/3 (0.6666...).
Since 0.618, the value of the golden ratio, is difficult to measure in an instant, but photography is the art of the moment, the rule of thirds is often applied instead of the golden ratio. To avoid the need to measure 0.618, photographers often use 2/3 and 1/3 instead. Digital cameras, such as smartphones, are particularly helpful for this, as their displays often show three grids next to or on top of each other, representing the thirds. To achieve interesting compositions, it can be useful to position the subjects along these lines rather than in the center.
However, the rule of thirds is not a universally applicable rule in photography, as 2/3 and the golden ratio are just two of several possible proportions. In professional photography, images are composed using various proportions, similar to painting. This may involve selecting proportionate backgrounds, furniture, or accessories in artistic portrait photography, for example, all of which are photographed from a fixed tripod to ensure that the final image is harmoniously proportioned overall.
Geometric construction
1
1
2
3
5
8
13
21
34
55
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
1
9
36
84
126
126
84
36
9
1
IV Golden Ratio according to Euclid
There are various methods to construct the golden ratio. The most well-known is that of the ancient mathematician Euclid (3rd century BC).
- Construction of a rectangle from two adjacent squares above the line segment AB (for the sake of clarity, the construction of the rectangle has been omitted here).
- Draw the diagonal of the rectangle.
- Measure the side length of one square along the diagonal.
- Transfer the other part of the diagonal to the original given line segment (light blue line).
- This divides the original line segment in the ratio of the golden ratio (yellow point).
The Golden Rectangle
When the minor segment is rotated by 90 degrees, it forms a golden rectangle, meaning that the side lengths are in the ratio of the golden ratio (Mouseover, orange rectangle).
V Regular Pentagon
The golden ratio is necessary to construct a regular pentagon. In a regular pentagon, all sides are of equal length.
Given a line segment AB, divided in the golden ratio at point D. Additionally, the perpendicular bisector of the line segment is needed (dashed vertical line through point M). For the sake of clarity, the construction of the perpendicular bisector is omitted here.
Left and right corner points of the pentagon
- correspond to the endpoints of the given line segment AB.
Upper corner point
- The minor DB of the golden ratio of the given line segment is taken as the radius of a circle centered at point D. A circle is drawn with this radius. Where it intersects the perpendicular bisector of the line segment AB, the upper corner point of the pentagon is located (upper blue point).
Lower right corner point
- A line is drawn from the upper corner point of the pentagon through the golden ratio point D on AB. The length of line segment AB is marked on this line, resulting in the lower right corner point F.
Lower left corner point
- A circle is drawn around the midpoint M of the given line segment AB, with a radius equal to the distance from the golden ratio point D to the midpoint M. The left intersection point of this circle with the given line segment AB gives us point C.
- A line is drawn from the upper corner point E of the pentagon through point C, and the length of line segment AB is marked on this line, resulting in the lower left corner point G.
Connecting these five corner points creates a regular pentagon (dark blue lines). The five diagonals of the pentagon form a five-pointed star, and these lines always intersect at the golden ratio points (light blue and orange lines).


VI Golden Spiral
The golden spiral is often represented in an approximation construction.
- Draw a line (bottom horizontal).
- Divide the line at the golden ratio (blue: golden ratio major, orange: golden ratio minor).
- From the golden ratio point of the line, draw a 90° angle clockwise. The length of this line must correspond to the golden ratio major of the original line.
- Divide this line also at the golden ratio, ensuring that the golden ratio minor aligns with the golden ratio of the first line (orange lines).
- Repeat this process infinitely (here, six more times).
- In each of the squares, draw a quarter circle so that the quarter circles touch.
- Draw two diagonals to determine the center of the spiral (mouseover/tap).

The golden number
The golden number indicates the division ratio of the golden section. It is usually denoted by the 21st Greek letter φ (Phi) and has the rounded value of 1.618. The golden number is an irrational number and therefore infinite. It is obtained by adding the length of the major of a line of length 1 divided in the golden section and the number 1, i.e. ~0.618 + 1 = ~1.618.
Calculation of the golden number
The numerical value of the golden ratio is derived from the geometric construction of the golden section according to Euclid and is represented by the length of segment AE (left figure).
This length can be calculated using the Pythagorean theorem since points ABC form a right-angled triangle.
The lengths of segments AB and BC are known since the rectangle is composed of two adjacent squares. Therefore, the height of the rectangle is exactly half of its width. Here, the width of the rectangle is 1 unit, so its height is 0,5 units.
The length of diagonal AC is determined by the Pythagorean theorem:
AC2 = AB2 + BC2
AC = 12 + 0,52 = 1,25 ≈ 1,118
The length of the golden section is obtained by subtracting segment DC from AC because DC, like BC, represents the radius of the circle centered at point C, and thus, it has a length of 0,5.
So, the length of AD and thus the value of the golden ratio is:
1/φ = AC - DC ≈ 1,118 - 0,5 ≈ 0,618
Variant with the square root of 5
Confusingly, the width of the rectangle is often not given as 1, but as 2. This also changes the height of the rectangle from 0,5 to 1. The same calculation with the new values:
AC = 22 + 12 = 5
AD = 5 - 1 = ~1,236
To get to the original numerical ratio of the golden section for a rectangle with the width of 1, this value must be divided by 2 (mouseover/tap). Although the distance AE divides the distance AB in the golden section, the latter has the length 2 and the golden section of length 1 is searched for. Consequently, AE must be divided in the point M, which leads to the searched size of 0,618 (Mouseover/Tap, yellow dot). Mathematically, this results in the following:
AD = (5 - 1) / 2 = ~0,618
From the geometrical consideration it is obvious that this method needs one step more. That it is nevertheless the more popular variant can only be explained by the fact that
1/φ = (5 - 1) / 2 is more pleasant to read than
1/φ = 1,25 - 0,5 from the previous calculation
Representation of the golden ratio on a number line from 0 to 3. It's evident that φ is derived from 1 and the value of the golden ratio, which is approximately 0,618
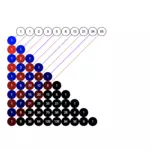
Fibonacci sequence and Pascal's triangle
1
1
2
3
5
8
13
21
34
55
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
1
9
36
84
126
126
84
36
9
1
VII The Fibonacci sequence
The Fibonacci sequence is named after the Italian mathematician Leonardo Fibonacci (c. 1170-1240). The sequence of numbers is obtained by adding the last two known numbers of the sequence together and adding this sum to the sequence, starting with zero and one.

The Fibonacci sequence is closely related to the Golden Ratio because the result of dividing two consecutive numbers in this sequence steadily approaches the Golden Ratio's division ratio, which is approximately 0,618.
| Calculation | Fibonacci sequence | Division ratio |
| 0 + 1 = 1 | 0,1 | 0/1 = 0 |
| 0 + 1 = 1 | 0,1,1 | 1/1 = 1 |
| 1 + 1 = 2 | 0,1,1,2 | 1/2 = 0,5 |
| 1 + 2 = 3 | 0,1,1,2,3 | 2/3 ≈ 0,666 |
| 2 + 3 = 5 | 0,1,1,2,3,5 | 3/5 = 0,6 |
| 3 + 5 = 8 | 0,1,1,2,3,5,8 | 5/8 = 0,625 |
| 5 + 8 = 13 | 0,1,1,2,3,5,8,13 | 8/13 ≈ 0,615 |
| ... | ||
| 89 + 144 = 233 | 0,1,1,...,144,233 | 144/233 ≈ 0,6180 |
VIII Pascal's triangle
The term "Pascal's Triangle" is attributed to the scientist Blaise Pascal (1623-1662).
Centered Representation
In this representation, the numbers in the triangle are generated such that each number is the sum of the two numbers directly above it. If there is only one number, the other is considered to be 0 (for the numbers on the outer edges of the triangle). The triangle starts with the number 1 at the top.
The centered representation of Pascal's Triangle was primarily used to expand binomial powers, such as
(a+b)2 = 1a2 + 2a1b1 + 1b2
Here, 1, 2, and 1 correspond to the numbers in the third row of Pascal's Triangle. The numbers in the subsequent fourth row (1, 3, 3, 1) can be used to expand the third power of the binomial (a+b), like so:
(a+b)3 = 1a3 + 3a2b1 + 3a1b2 + 1b3
and so on.
Left-Aligned Representation
Pascal's Triangle can also be represented in a left-aligned format. This makes it easier to read the sequences of numbers contained within.
2nd Column: Natural numbers
3rd Column: Triangle numbers
4th Column: Tetrahedral numbers
The Fibonaci sequence in Pascal's triangle
The Fibonacci number sequence arises from the sum of the numbers lying on a diagonal at a 45° angle when Pascal's Triangle is represented in the left-aligned format.
The greatest pleasure is knowledge.







![[Translate to english:] [Translate to english:]](/fileadmin/_processed_/8/b/csm_leonardo-alle-gemaelde_2dc4b01ef6.webp.pagespeed.ce.ohfmgl8OfF.webp)